Excel-10: 平均・分散・標準偏差



理系のためのExcelグラフ入門 表紙 金丸隆志「理系のためのExcelグラフ入門」好評発売中です

グラフの例

本ページの目的は、平均と標準偏差の使いどころを理解することであるが、
そのために、再び「振動実験」のグラフを描くことを例にとろう。

まず、excel_data00.xlsx というファイルをダウンロードし、各自のマイドキュメントに保存してほしい。
(マウス右クリックから「対象をファイルに保存」が確実。)

その後、ファイルをダブルクリックすると以下のようなデータが現れる。
下のデータは、振動実験を10回行った結果を表にまとめたものである。



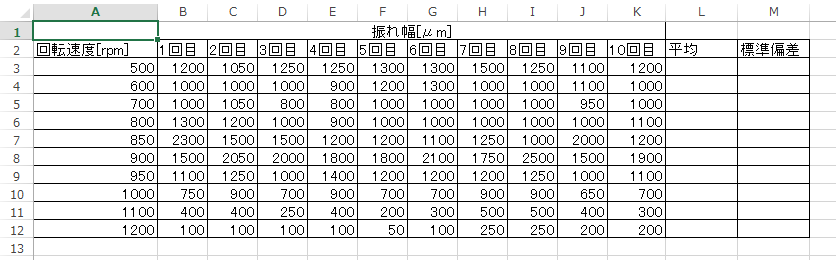
どのようなグラフだったか思い出すため、２回分のデータだけグラフを描いてみよう。
まず、「回転速度」「１回目」「２回目」のデータをマウスで選択する。



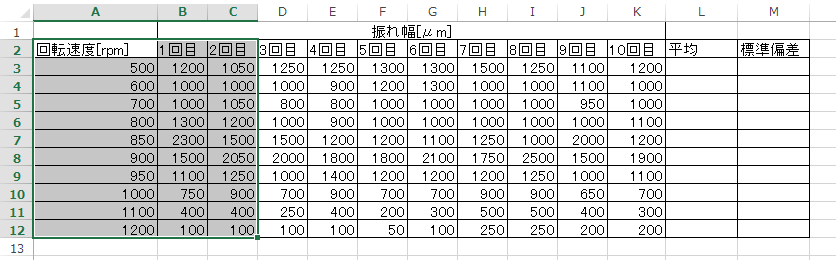
そして、「挿入」タブ→「散布図」→「散布図(直線とマーカー)」を選択すると、下図のようなグラフが現れる。
本来ならばここでグラフタイトルや軸ラベルなどを記すのであるが、今はグラフの形を確認したかっただけなので、それは省略する。



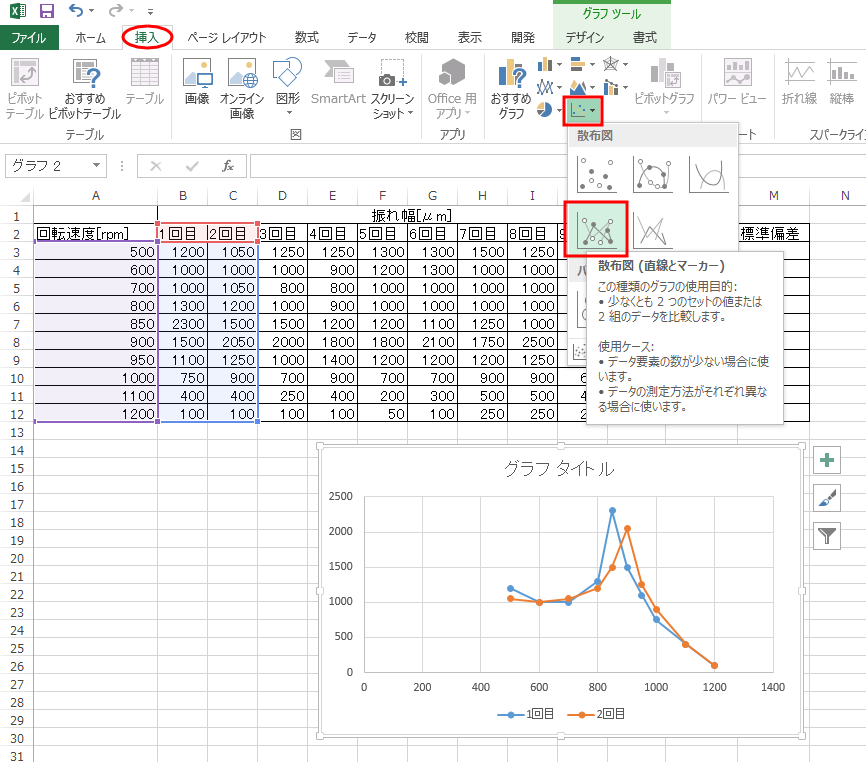
なお、学生が実験で描いたグラフを見ると「マーカー(データポイント)がないもの」や「マーカー(データポイント)が曲線で結ばれているもの」をしばしば見かける。
しかし、データポイントは皆さんが計測したデータそのものであるから重要である。
そのため、データポイントがあるグラフでなければならない。

また、曲線でデータポイントを結ぶのが好ましくない場合がある。
なぜかというと、そもそも実験でわかるのは、データポイントにおけるデータだけである。
データポイントの間でどのようなデータが得られるかは厳密に言えばわからない。
そこを曲線で結ぶと言うのは、データに先入観を与えることになり、好ましくない場合がある。

この考え方を突き詰めれば、データを直線で結ぶのも好ましくないという考え方もでき、
実際、データポイントだけを表示して、線で結ばないグラフもしばしば見られる。
そのあたりは適材適所で、適宜判断していこう。


10 回分のグラフを描いてみる

それでは、話を先に進めよう。10回の実験を行った場合、それらをどのようにグラフ化すれば良いだろうか？

まずは、シンプルに１０回分のグラフを重ね書きしてみよう。
10回分のデータをマウスで選択し、上でやったのと同じようにグラフを挿入すればよい。

すると、以下のように先程とは全く異なる形のグラフになってしまう。
これは、下図において青色のデータ (10 個) を x 軸にしたかったのに対し、
赤色のデータ (11 個)が x 軸として自動選択されて しまったためである。
(どちらが x 軸として選ばれるかはデータの個数による)



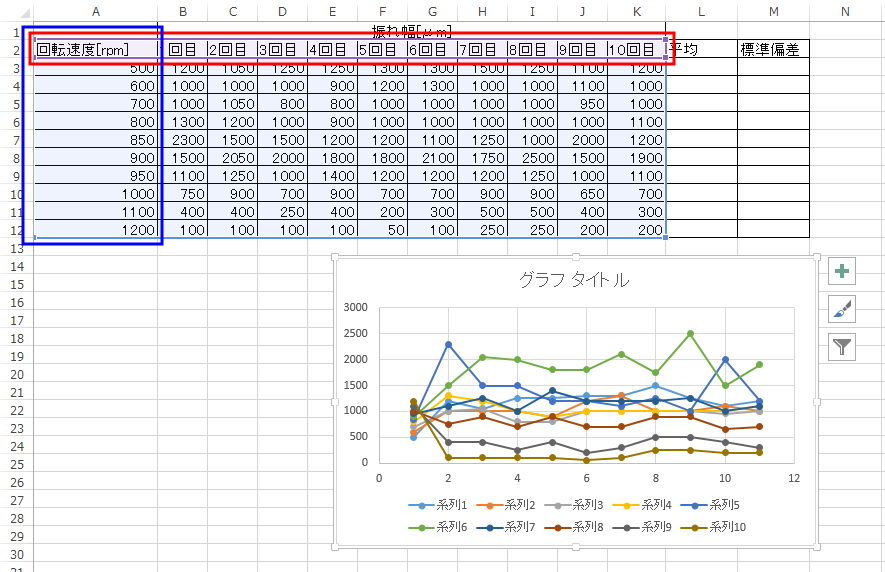
こういうときは慌てずにグラフを選択した上で、 「デザイン」タブから「行/列の切り替え」を選べば良い。



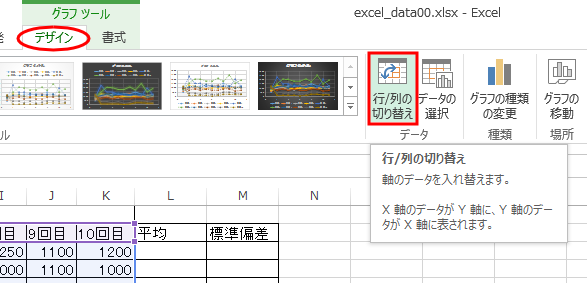
そうすれば、x 軸を正しく指定できたことになり、10 系列のグラフが描ける。 (グラフの設定はまだ省略している)



しかし、(ここからがこのページの本題であるが) この10本のグラフは データとして有用であると言えるだろうか？
少なくとも、10本のデータを一つ一つ見分けることは困難であることが わかるだろう。

このような場合、平均と標準偏差をうまく利用して図示化すると、
10本のデータの性質が良く分かるようなグラフを描くことができる。


平均と標準偏差を図示してみよう

ここから本ページの本題。

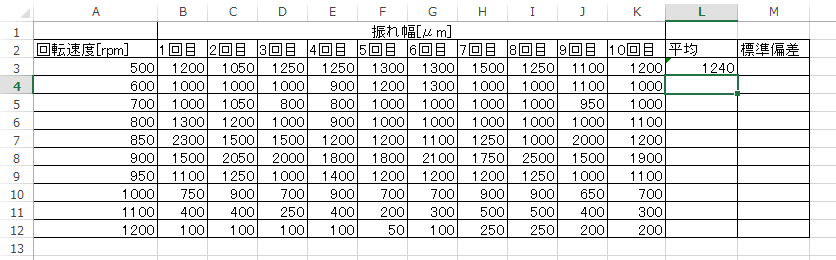
まず、10 回分のデータの平均を求めよう。平均は AVERAGE 関数で求められる。

今、下図の回転速度 500 [rpm] の10回分のデータの平均を求めるには、 下図のように「=AVERAGE(B3:K3)」と入力すれば良い。



正しく入力できれば、以下のように平均値が計算される。
このセルをコピーして下の全てのセルに貼り付ければ全ての入力に対する平均計算が完了する。
これはExcel の相対参照の考え方により可能なのだった。

それを簡単に行うには、「セルL3を一回クリックし、そのセルの右下のフィルハンドル(■)をダブルクリックする」のが簡単である。



やってみると下記のようになる。



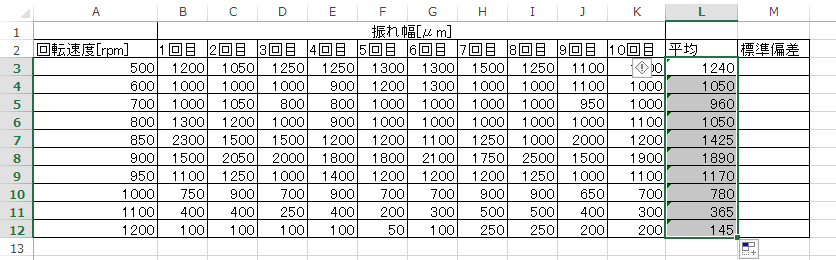
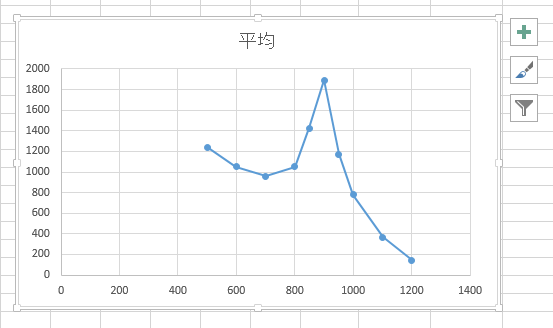
まず、この平均をグラフ化してみよう。

まず、回転速度の列と平均の列を同時選択する。
同時選択するには、まず「回転速度」の列をマウスでドラッグして選択した後、
Ctrl キーを押しながら「平均」の列をマウスでドラッグして選択すれば良い。



そして、「挿入」タブから散布図のグラフを描けば下図のように平均のグラフが得られる。
しかし、せっかく10回分実験したのに、平均のグラフしか描かないのはもったいない。
標準偏差は、10回の実験のバラツキの程度を数値化したものである。それも図に取り込んでみよう。



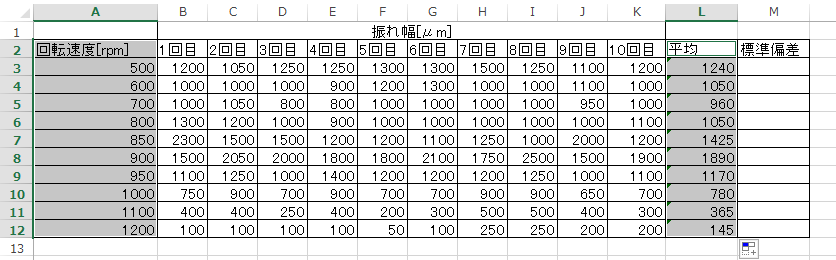
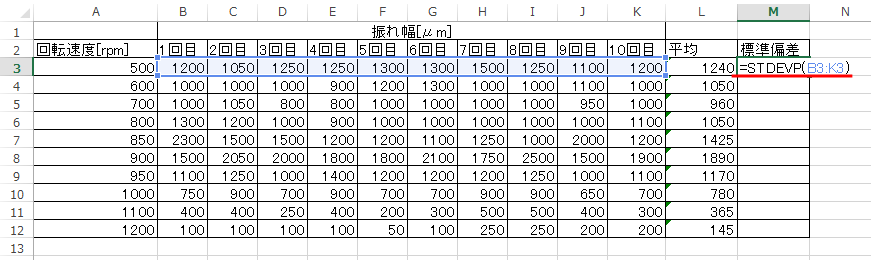
まず、標準偏差をを計算しよう。これを STDEVP 関数で求める。
AVERAGE と同じように、全てのセルで計算 (コピー) しよう。



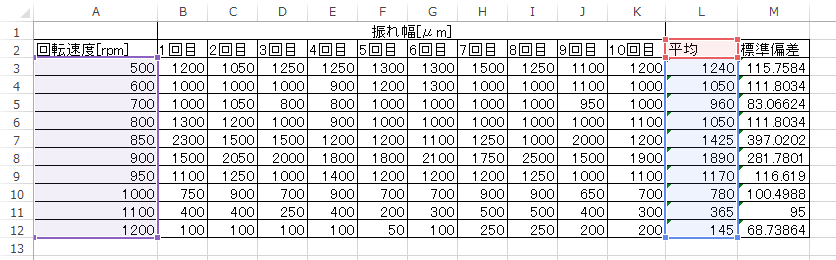
下図のように計算が標準偏差の計算が完了する。



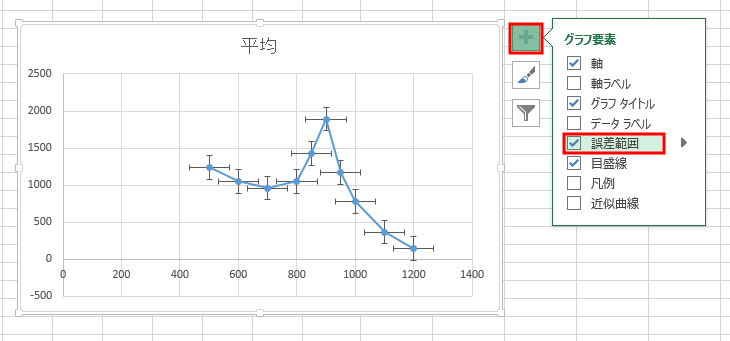
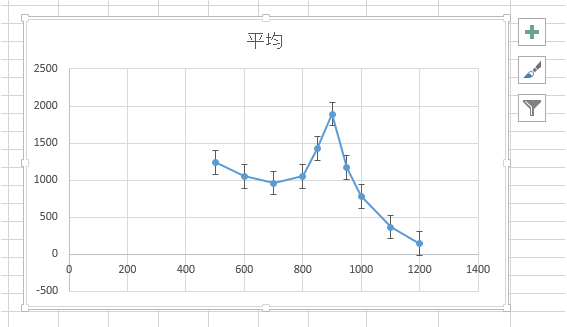
ここで、平均値のグラフにおいて、下図のようにグラフ要素の「誤差範囲」をチェックして追加しよう。
データの各点に誤差範囲を示す十字が現れる。

ただし、この時点ではデータの標準偏差に無関係な範囲が表示されているだけなので、ここで満足しないよう注意しておく。



実現したいのは、データの縦軸方向の誤差範囲を標準偏差で図示することである。
しかし、現時点では縦軸だけではなく横軸にも誤差範囲が表示されている。 これは邪魔なので消してしまおう。

そのためには、まず、横軸方向の誤差範囲をマウスで選択しよう。



そしてキーボードのDelキーを押す。すると、縦軸だけの誤差範囲となった。
しかし、繰り返すが、この時点ではデータの標準偏差に無関係な範囲が表示されているだけなので、やはりここで満足しないよう注意しておく。



ここから、既に上で計算した標準偏差をグラフ中の誤差範囲に反映させる作業に入る。
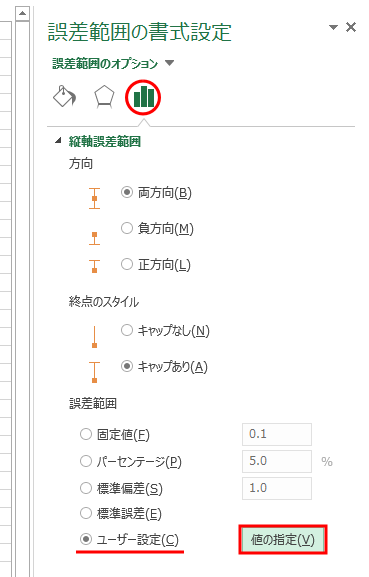
まず、下図のようにグラフ要素の「誤差範囲」から「その他のオプション」を選択する。



すると、下図のように、右側に「誤差範囲の書式設定」という画面が現れる。
下にあるユーザー設定の「値の指定」ボタンをクリックしよう。



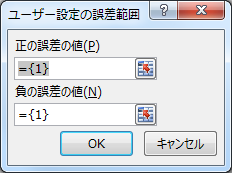
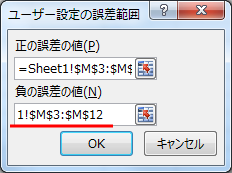
すると、以下のように誤差範囲を指定するダイアログが現れる。
ここで先程計算した標準偏差を指定することになる。



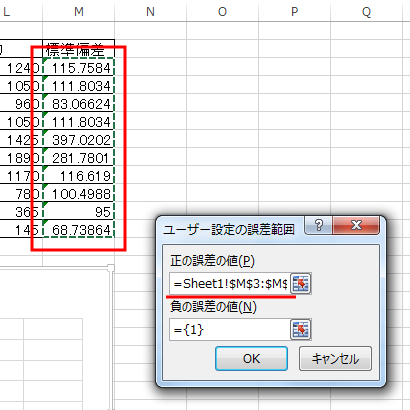
上図のように「正の誤差の値」の記入欄が色が反転して選択された状態で、 下図のように標準偏差の領域をマウスでドラッグして選択しよう。
すると、「正の誤差の値」の部分に領域を表す式が格納される。



同様に、「負の誤差の値」の記入欄をマウスで選択し、
下図のように色が反転した状態で同じ「標準偏差」の領域をマウスでドラッグして選択すると、



やはり「負の誤差の値」の部分に領域を表す式が格納される。 ここでOKボタンをクリックすると標準偏差がグラフ化される。



触れ幅最大付近の 800[rpm]、900[rpm] では、データのばらつきが大きいことが見てとれるだろう。



これを、レポートに耐え得るように細かく設定することで、 最終的に以下のようなグラフにすることができる。



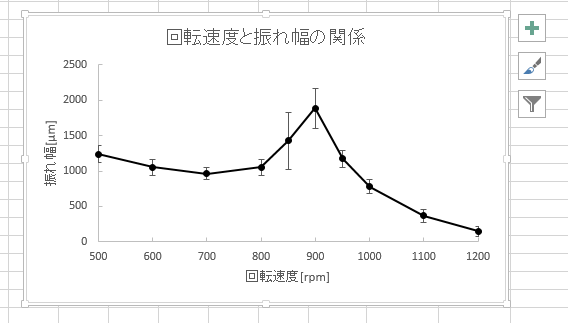
参考までに、上のグラフで設定した箇所をまとめると下記のようになる。
面倒に思えるかもしれないが、他人が見てわかりやすいグラフを作成しようと思うとこれくらいの設定は必要となる。 グラフの設定法を忘れた場合は、以下のページを復習して欲しい。

←Excel-09-2: SUM 関数で数列の和を計算する／ Excel-11: 絶対参照とは何か～グラフの例をもとに→

Microsoft Office の基礎に戻る