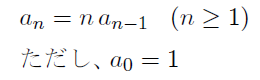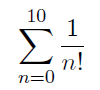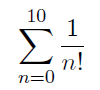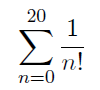Excel-09-2 SUM 関数で数列の和を計算する
前ページではテストの合計点や平均点を関数を用いて計算した。
本ページでは、SUM 関数をより数学的な例に用いてみよう。
具体的には、Excel で「数列」を計算し、数列の和を SUM 関数で求めてみる。
本ページでは以下のように 4 問の演習を通して解説を進めて行く。
まずは簡単な例として、以下の漸化式に基づく数列 an の n=10 の項までを Excel で計算してみよう。

A 列を 0 以上の整数 n、B 列を an を表示するために用いることにしよう。
まず、見出しとして以下のように記入する。

n = 0 から 10 までの an を計算するのであるから、A 列には 0 から 10 の整数を記入しよう。
オートフィルが使えるので、まずはセル A2 とセル A3 にそれぞれ 0 と 1 を記入。
その後、下図のようにセル A2 とセル A3 を同時選択し、フィルハンドルを掴んで下に移動する。

すると、以下のように n の値として 0 から 10 を記入できる。
手作業で入力せず、オートフィルを覚えてマスターすること!

次に、下図のようにセル B2 に初項である a0=0 の値 0 を記入する。

次に、セル B3 に、漸化式「an = -2 an-1 + 1」に対応する式である
「 = -2*B2+1 」を記入する。ここでは答えを教えてしまっているが、この式を自分で思い付けるかどうかがポイント。
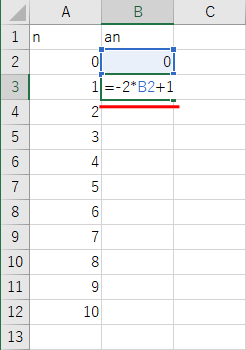
記入が終わったら Enter キーを入力すると、式の値である 1 が計算され表示される。

後は、式を記入したセル B3 を選択し直し、フィルハンドルを掴んでオートフィルすることで…、
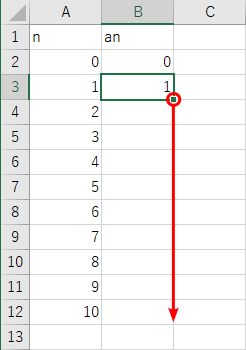
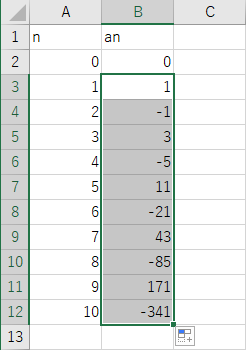
数列 an の n=10 までの計算が完成する。
なお、ここで行ったオートフィルは「セル B3 を Ctrl-C でコピーし、セル B4 から B12 に Ctrl-V で貼り付け」したのと同じである。
もう少し難しい漸化式の例として、階乗 n! の値を漸化式を利用することで計算してみよう。
階乗を an=n! のように数列と見なすと、an は以下の漸化式を満たす。0! = 1 であることにも注意。
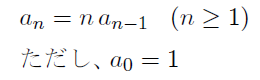
この漸化式を Excel で n=10 まで計算してみよう。
先程の演習の続きとして、下図のように E 列と F 列を用いることにしよう。
E 列にオートフィルで n=0 から 10 までの値を記入しよう。
F 列には、セル F1 に見出しとして「n!」と書いておく。
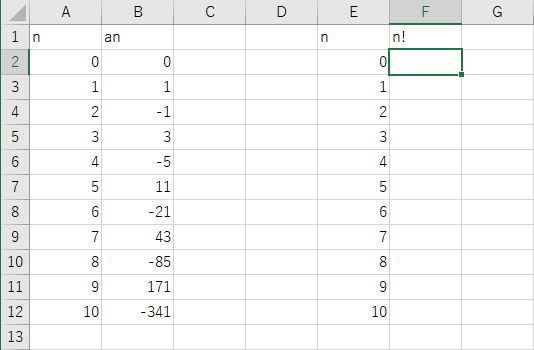
次に、セル F2 に、a0=1 (すなわち 0!=1) に対応する値 1 を記入しよう。

次に、セル F3 に、漸化式「an = n an-1」に対応する式
「 = E3*F2 」を記入する。ここでは答えを教えてしまっているが、この式を自分で思い付けるかどうかがポイント。

式を書けたら Enter キーを押すことで、式が計算されその値が表示される。

後は、式を記入したセル F3 を選択し直し、フィルハンドルを掴んでオートフィルすることで…、
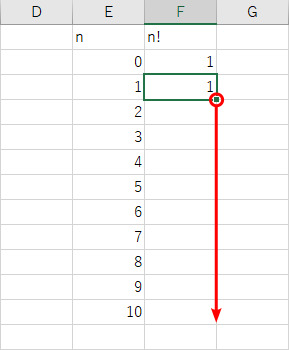
数列 an 、すなわち階乗 n! の n=10 までの計算が完成する。
なお、ここで行ったオートフィルは「セル F3 を Ctrl-C でコピーし、セル F4 から F12 に Ctrl-V で貼り付け」したのと同じである。

次に、数列 1/n! の、n=0 から 10 までの項の和、
すなわち次式を Excel で計算してみよう。ここで本ページの本題である SUM 関数を用いるのである。
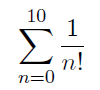
演習 2 で数列 n! は計算済なので、数列 1/n! の計算は (Excel を十分理解していれば) 簡単にできる。
下図のように、演習 2 の続きとして、G 列に数列 1/n! を表示することにしよう。
見出しとして、セル G1 に「 1/n! 」と記入する。
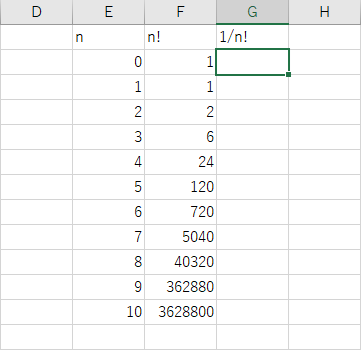
数列 1/n! は、数列 n! の逆数なのであるから、セル G2 に「 = 1/F2 」と記入すればよい。

式を書けたら Enter キーを押すことで、式が計算されその値が表示される。
後は、式を記入したセル G2 を選択し直し、フィルハンドルを掴んでオートフィルすることで…、
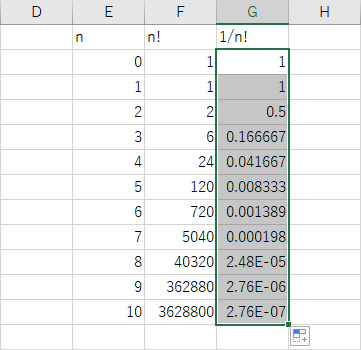
数列 1/n! の n=10 までの計算が完成する。
なお、ここで行ったオートフィルは「セル G2 を Ctrl-C でコピーし、セル G3 から G12 に Ctrl-V で貼り付け」したのと同じである。
シート上に見える、「2.48E-05」という数値は、「2.48×10-5」、すなわち「0.0000248」を意味する。
つまり、「2.48E-05」の「E」より右側の数値は、「10 の何乗か」を表す数である。
さて、ここからが本題。
数列 1/n! の n=10 までの和を計算しよう。
見出しとして、セル H1に「n=10 の項までの和」と記入しよう。
後のために、「H」と「I」の間の境界線を掴んでセルの幅を広げておいた方が良い。
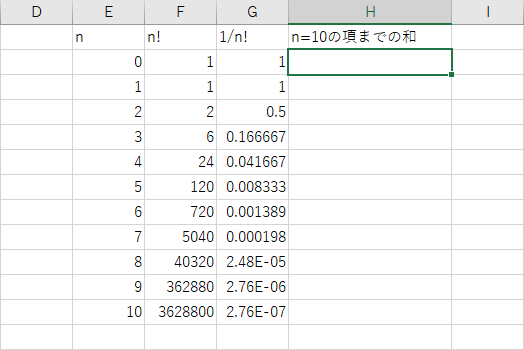
今、セル G2 から セル G12 の値 (すなわち、数列 1/n! の、n=0 から n=10 までの値) を合計したいのであるから、
セル H2 に「 = SUM(G2:G12) 」と記入すれば良い。
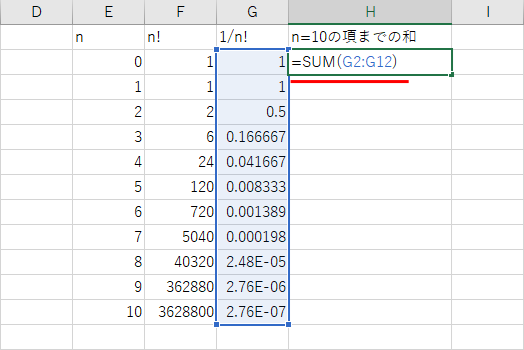
式を書けたら Enter キーを押すことで、式が計算されその値が表示される。
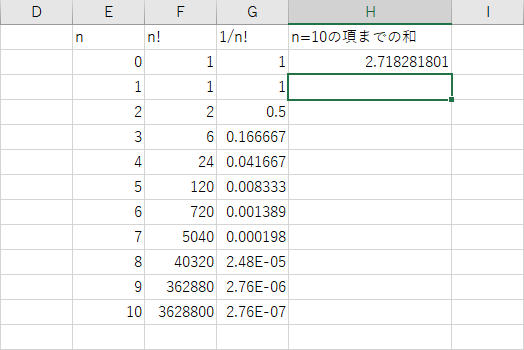
さて、皆さんがここで計算したのは
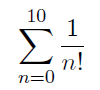
であるが、この和の計算を n=∞ まで行うと、その和の極限はネイピア数 e となることが知られている。
インターネットでネイピア数 e の値を調べ、皆さんが計算した値が小数第何位までネイピア数と一致するかを、
下図のように記入しよう。
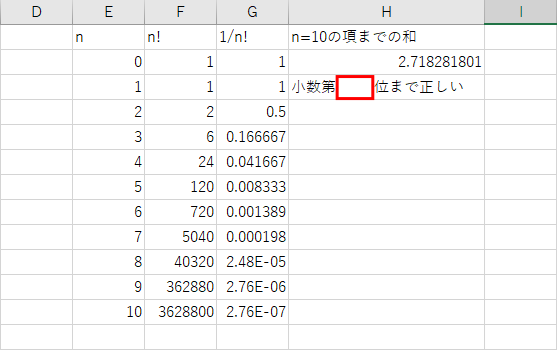
最後に、数列 1/n! の和の計算を、「n=0 から 10 まで」から「n=0 から 20 まで」に変更しよう。
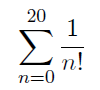
n=10 までの計算を流用する方針で演習を行うと、Excel シートは下図のようになるだろう。
シートを完成させよ。

←Excel-09: SUM 関数と AVERAGE 関数/
Excel-10: 平均・分散・標準偏差→
Microsoft Office の基礎に戻る