 For these themes, please see the following pages.
For these themes, please see the following pages.
 Moreover, properties of neurons consisting of the brain, and structures of networks are not uniform. To analyze such systems, the probabilistic representation is crucial to understand their dynamics.
Moreover, properties of neurons consisting of the brain, and structures of networks are not uniform. To analyze such systems, the probabilistic representation is crucial to understand their dynamics.
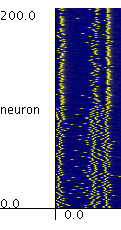
 For example, let us consider a system consisting of 200 neurons as shown in the right figure. Because noise is injected to the system, each neuron fires randomly (shown with red points).
Although it is difficult to analyze such stochastic systems directly,
we can obtain the Fokker-Planck equation that governs the time-development of the probability density of the system in the limit of large number of neurons.
For example, let us consider a system consisting of 200 neurons as shown in the right figure. Because noise is injected to the system, each neuron fires randomly (shown with red points).
Although it is difficult to analyze such stochastic systems directly,
we can obtain the Fokker-Planck equation that governs the time-development of the probability density of the system in the limit of large number of neurons.
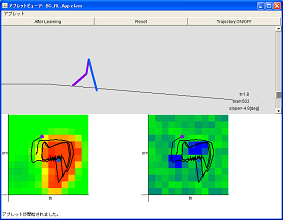 Let us consider movements of human, such as biped walking.
Although there are several conditions
for walking, such as "walking on the flat ground",
"walking on the graveled ground",
"ascending/descending the stairs",
"going up/down the slope", and so on,
we can walk stably regardless of the conditions.
Let us consider movements of human, such as biped walking.
Although there are several conditions
for walking, such as "walking on the flat ground",
"walking on the graveled ground",
"ascending/descending the stairs",
"going up/down the slope", and so on,
we can walk stably regardless of the conditions.
 Unlike the Fourier transformation, the wavelet transformation is suitable for spatially and temporally localized signals such as images.
Unlike the Fourier transformation, the wavelet transformation is suitable for spatially and temporally localized signals such as images.