[Excel で VBA] 微分方程式の数値的解法 (2) VBA + Excel

前ページに引続き、微分方程式の数値解法を学ぶ。
本ページでは VBA のプログラミング機能を用いて実現する。

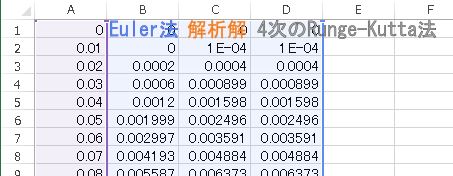
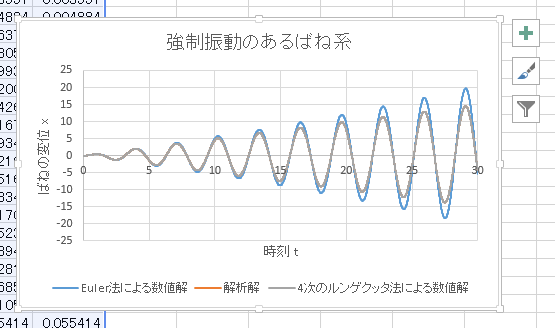
Excel / OpenOffice で学ぶフーリエ変換入門 表紙 「Excel / OpenOffice で学ぶフーリエ変換入門」では本章で解説する微分方程式の数値的解法を用いたマクロを
ソースを閲覧可能な形で収録しております。

Euler 法

本ページの学習に入る前に、前ページの Excel シートを保存して閉じておこう。
本ページのプログラムを記述する際は、新しいファイルでスタートするようにして欲しい。

さて、Excel の場合と同様、Euler 法での数値積分を実現するのが 以下の VBA プログラムである。

ポイントは 記述して実行してみよう。
(Visual Basic Editor の起動方法は「第一回：プログラムを書き始めるまでの準備」参照)



実際にプログラムを書いてみて、以下のことに気づいただろうか。

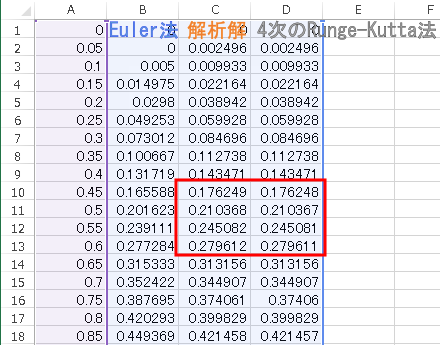
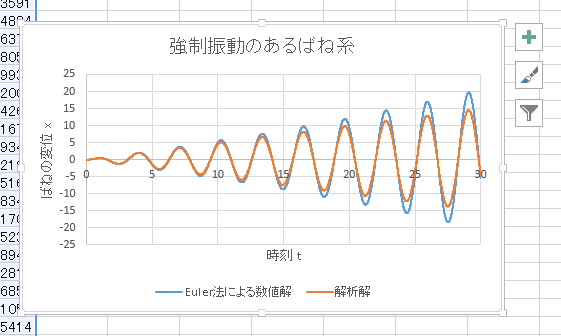
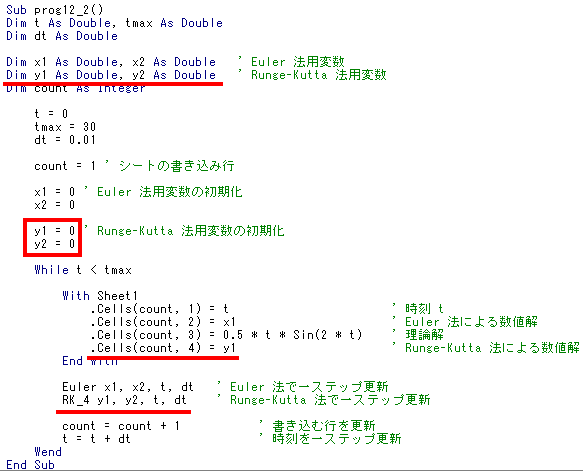
f2(x1, x2, t) = -4 x1 + 2 cos(2t) という式を実現するため、
前ページの Excel のみの手法では

-4*B2+2*cos(2*A2)

と記述したのに対し、今回の VBA では、

-4*x1+2*cos(2*t)

と記述できる。

つまり、Excel では変数名として B2 や A2 といったセル番号を用いねばならないのに対し、
VBA では t や x1 などという、元の式に近い変数を (宣言すれば) 使える。

Excel のみの時のように、B2 や A2 という抽象的な変数名で式を記述することは (実際にやってみるとすぐにわかることだが)、
非常にわずらわしく、間違いが混入しやすい。

一方、VBA のようにある程度分かりやすい変数名でプログラミングできれば、 間違いが起こりにくく、また計算の内容も非常にわかりやすい。
(もちろん、Visual Basic というプログラミング言語にある程度慣れていなければならないという制約はある)

そのようなわけで、ある程度複雑な処理をしようとすると、Excel のみで頑張るよりも、
Visual Basic を利用した方が逆に簡単になる場合がある、ということに気づいてもらえると嬉しい。

さて、プログラムを記述して実行してみよう。
Visual Basic Editor 上では何も変化が起こらないが、
通常の Excel に戻ってみると、以下のように 3 列のデータがプログラムにより 書き込まれている。
(色つきの文字はこちらで記入したものであるので、皆さんの Excel では表示されない)

これらは、左から順に「時刻」、「Euler 法による数値解」、「解析解」である。



このグラフを描くために、3 列を選択しよう。
「A」から「C」をマウスをドラッグするように選択するか、
「A」を一回クリックした後、「Ctrl キーを押しながら、『B』、『C』を一回ずつクリック」すると良いのだった。



そしてグラフウィザードを起動して散布図を選択する。
得られるグラフは以下のようになる。(下図は若干の調整を済ませてある)

Excel のみの時と同様、Euler 法による数値解と解析解とには大きな誤差があることがわかる。




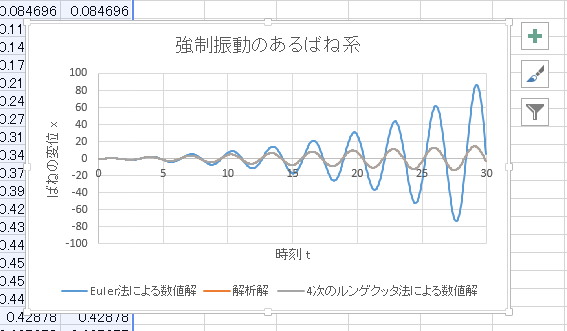
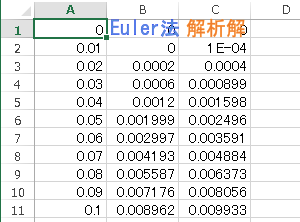
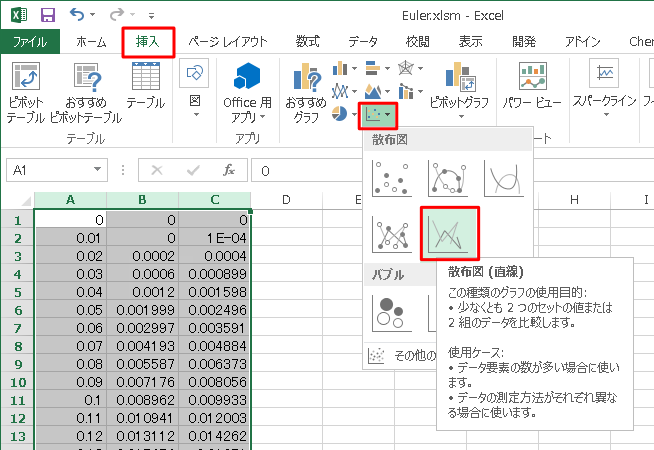
！Excel 2007 に関する注意！
このように本ページのプログラムを実行するとExcel シートにデータが表示され、
それをグラフに表示することができる。

多くの場合このまま作業を続けて良いのだが、 Excel 2007 を使う場合はグラフを表示したままプログラムを再実行すると
処理に非常に長い時間がかかり、パソコンがフリーズしてしまうこともある。

そのため、Excel 2007 を使う場合、グラフを一度表示して確認したら
キーボードの Delete キーでグラフを削除してしまうのが無難である。

もし誤ってグラフを表示したままプログラムを実行してしまったら、
キーボードの Esc キーか、Ctrl+Pause キーで急いで退避しよう。

いちいちグラフを消去するのが面倒だという場合 (もっともな意見)、 While ～ Wend の前後に以下のように命令を付加すれば良い。 

    Application.ScreenUpdating = False     'この行追加
    While t < tmax
    …
    Wend
    Application.ScreenUpdating = True     'この行追加

これにより、シートへのアクセス中はシートとグラフの更新が行われず、
シートへのアクセスが完了してからシートとグラフの更新が行われるようになるため、
Excel 2007 でいちいちグラフを削除しなくても処理が正しく終了する。

4 次の Runge-Kutta 法

誤差の大きい Euler 法に代わって広く使われているのが4 次の Runge-Kutta 法である。

4 次の Runge-Kutta 法の細かな式はここでは重要ではないが、興味のある人は このリンク先を見て欲しい。

さて、プログラム全体を記述すると以下のようになるが、これを全て書くのは大変なので、 以下で簡単に実行できる方法を示す。




上のプログラムを記述する前に、まず本ページ最上部の Euler 法のプログラムを記述しよう (これは各自で記述して欲しい)。

記述できたら、以下の赤の部分 (4 箇所) を追加して欲しい。



そして、プログラムの末尾に、以下の枠内の内容をコピーして貼り付けて欲しい。
これでプログラムが完成する。 

Sub RK_4(x1 As Double, x2 As Double, t As Double, dt As Double)

Dim k11 As Double, k12 As Double
Dim k21 As Double, k22 As Double
Dim k31 As Double, k32 As Double
Dim k41 As Double, k42 As Double

    k11 = dt * func1(x1, x2, t)
    k12 = dt * func2(x1, x2, t)
    
    k21 = dt * func1(x1 + k11 / 2, x2 + k12 / 2, t + dt / 2)
    k22 = dt * func2(x1 + k11 / 2, x2 + k12 / 2, t + dt / 2)
    
    k31 = dt * func1(x1 + k21 / 2, x2 + k22 / 2, t + dt / 2)
    k32 = dt * func2(x1 + k21 / 2, x2 + k22 / 2, t + dt / 2)
    
    k41 = dt * func1(x1 + k31, x2 + k32, t + dt)
    k42 = dt * func2(x1 + k31, x2 + k32, t + dt)

    x1 = x1 + (k11 / 6 + k21 / 3 + k31 / 3 + k41 / 6)
    x2 = x2 + (k12 / 6 + k22 / 3 + k32 / 3 + k42 / 6)

End Sub

Function func1(x1 As Double, x2 As Double, t As Double)
    func1 = x2
End Function
 
Function func2(x1 As Double, x2 As Double, t As Double)
    func2 = -4 * x1 + 2 * Cos(2 * t)
End Function


このプロシージャ RK_4 の意味を理解する必要は本講義ではないが、以下のことは注意しておいて欲しい。

RK_4 は見たところ行数も多く複雑に思えるが、式と比較しながら注意深く観察すれば、
理解できないほどの複雑さではない。変数名と式にある程度対応がつけられるからである。

一方、これを Excel のシートのみで実現しようとすると、不可能ではないが非常に大変である。
(Euler 法の計算のために 「t」、「x1」、「x2」、「f1」、「f2」の５列を利用したが、
4 次の Runge-Kutta 法には何列のデータが必要だろうか？)

このように、ある程度簡単な計算なら Excel のみの機能で十分であるが、
複雑な計算になると、VBA を用いた方が簡単な場合がある。

さて、プログラムを実行して Excel のシートに戻ると、以下のように 4 列のデータが完成している (文字は出ないので注意)。
左から順に 「時刻」、「Euler 法による数値解」、「解析解」、「4 次の Runge-Kutta 法による数値解」である。

グラフを描くために 4 列を同時選択して、グラフウィザードを起動して散布図を選択する。



すると、以下のようなグラフが得られる (下図は若干の調整済み)。

「解析解」と「4 次の Runge-Kutta 法による数値解」はほぼ同じ値を取って重なっているため、
ピンクの解析解が見えなくなっている。

すなわち、4 次の Runge-Kutta 法は Euler 法に比べると精度が非常に高いことがわかる。



最後に、時間刻み幅 dt を変えてシミュレーションを行うとどうなるかも調べておこう。
そのため、一旦データを消去しよう。4 列選択した状態で Delete キーを押すと



データが消える。



そこで、プログラムの下図の部分を 0.01 から 0.05 に変更してみよう。



そして、プログラムを実行し、Excel シートに戻ると新しいグラフが描かれている。

時間刻み幅を粗くしたので、Euler 法と解析解との差はますます大きくなっていることがわかるが、
4 次の Runge-Kutta 法は依然として解析解と重なっていることがわかる。



ただし、誤差が全くないわけではなく、データを注意深く見ると、
下図のように、若干の誤差がみられる。






←微分方程式の数値的解法 (1) Excel のみの方法／ 微分方程式の数値的解法 (3) 汎用性を高める→

Excel で学ぶ Visual Basic for Applications (VBA)に戻る