Sub make_vdP()
Dim t As Double, dt As Double, tmax As Double
Dim cellindex As Long, count As Long
Dim dimension As Integer
dimension = 4 ' 微分方程式の次元
Dim x() As Double
ReDim x(dimension - 1) As Double
t = 0: dt = 0.01: tmax = 30 ' 時刻に関する変数の初期化
x(0) = 0.5: x(1) = 0: x(2) = 0.6: x(3) = 0 ' 変数初期化
Dim writeRate As Long
writeRate = 5 ' 5 回に1回書き込み
Sheet1.Cells(1, 1).Value = "t" ' 1行目
Sheet1.Cells(1, 2).Value = "x1"
Sheet1.Cells(1, 3).Value = "y1"
Sheet1.Cells(1, 4).Value = "x2"
Sheet1.Cells(1, 5).Value = "y2"
cellindex = 2: count = 0
Application.ScreenUpdating = False
While t < tmax
If count Mod writeRate = 0 Then ' writeRate 回に1回だけシートに書き出し
Sheet1.Cells(cellindex, 1).Value = t
Sheet1.Cells(cellindex, 2).Value = x(0)
Sheet1.Cells(cellindex, 3).Value = x(1)
Sheet1.Cells(cellindex, 4).Value = x(2)
Sheet1.Cells(cellindex, 5).Value = x(3)
cellindex = cellindex + 1
End If
nextStep t, x, dt, dimension
t = t + dt
count = count + 1
Wend
Application.ScreenUpdating = True
Erase x
End Sub
Sub get_deriv(t As Double, x() As Double, dxdt() As Double)
Dim epsi1 As Double, epsi2 As Double
Dim g As Double
Dim gamma As Double
epsi1 = 0.17
epsi2 = 0.17
g = 0.1
gamma = 3.5
dxdt(0) = gamma * (epsi1 * (x(0) - x(0) ^ 3 / 3) - x(1) - g * (x(2) - x(0)))
dxdt(1) = gamma * x(0)
dxdt(2) = gamma * (epsi2 * (x(2) - x(2) ^ 3 / 3) - x(3) - g * (x(0) - x(2)))
dxdt(3) = gamma * x(2)
End Sub
Sub nextStep(t As Double, x() As Double, dt As Double, dimen As Integer)
Dim i As Long
Dim dxdt() As Double
Dim xout() As Double
ReDim dxdt(dimen - 1)
ReDim xout(dimen - 1)
get_deriv t, x, dxdt
rk4 t, x, dxdt, xout, dt, dimen
For i = 0 To dimen - 1
x(i) = xout(i)
Next i
Erase dxdt
Erase xout
End Sub
Sub rk4(t As Double, x() As Double, dxdt() As Double, xout() As Double, dt As Double, dimen As Integer)
Dim i As Long
Dim dth As Double, dt6 As Double, th As Double
Dim x2() As Double
Dim dxdt2() As Double
Dim dxdt3() As Double
ReDim x2(dimen - 1)
ReDim dxdt2(dimen - 1)
ReDim dxdt3(dimen - 1)
dth = dt * 0.5
dt6 = dt / 6#
th = t + dth
For i = 0 To dimen - 1
x2(i) = x(i) + dth * dxdt(i)
Next i
get_deriv th, x2, dxdt2
For i = 0 To dimen - 1
x2(i) = x(i) + dth * dxdt2(i)
Next i
get_deriv th, x2, dxdt3
For i = 0 To dimen - 1
x2(i) = x(i) + dt * dxdt3(i)
dxdt3(i) = dxdt3(i) + dxdt2(i)
Next i
get_deriv t + dt, x2, dxdt2
For i = 0 To dimen - 1
xout(i) = x(i) + dt6 * (dxdt(i) + dxdt2(i) + 2# * dxdt3(i))
Next i
Erase x2
Erase dxdt2
Erase dxdt3
End Sub
|
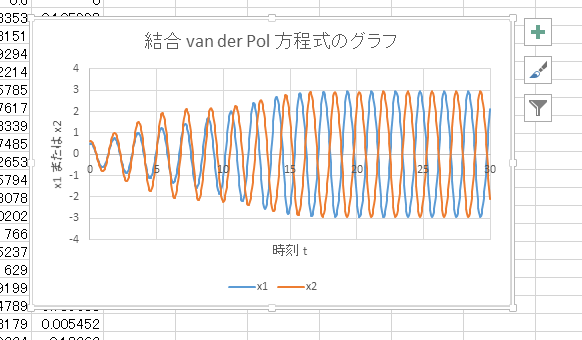
 「Excel / OpenOffice で学ぶフーリエ変換入門」では本章で解説する微分方程式の数値的解法を用いたマクロを
「Excel / OpenOffice で学ぶフーリエ変換入門」では本章で解説する微分方程式の数値的解法を用いたマクロを