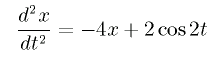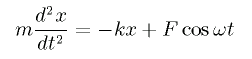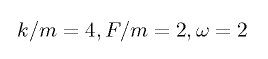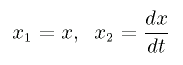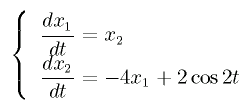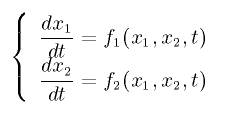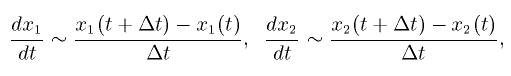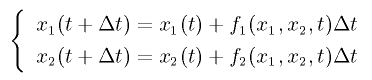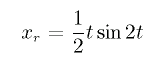[Excel で VBA] 微分方程式の数値的解法 (1) Excel のみの方法
前回、VBA から Excel のシートにアクセスする方法を学んだ。
この機能を用いると、様々な数学的な操作を Excel 上で行うことができるようになる。
ここでは「微分方程式の数値解法」を取り上げ、VBA (および Excel) 学習の総仕上げとする。
微分方程式の数値的に解くのは、「Excel のみを使う方法」と「VBA と Excel を組み合わせて使う方法」のどちらでもできる。
ここではその両方を取り上げ、その違いを体感してもらう。
本日取り扱う微分方程式は以下のものである。
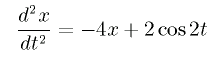
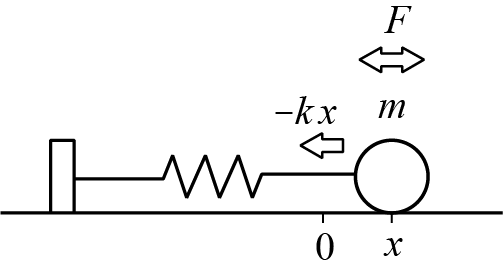
この微分方程式は、ばね系に周期的な外力が加わっている系の運動方程式
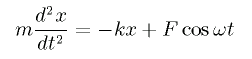
において、質量 m、ばね定数 k、外力の大きさ F、外力の振動数 ω に対し、
以下の制限を設けたものである。
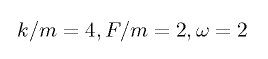
イメージ図を以下に示す。
この微分方程式 (運動方程式) は 2 階微分を含むが、これを数値的に解くためには
1 階微分のみの微分方程式に変換する必要がある。
そこで、以下の 2 変数 x1、 x2 を導入する。
(それぞれ、ばねの変位、速度を表す)
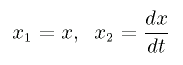
これらについて、以下の 1 階微分方程式が成り立つ (確認してみるとよい)。
(微分の階数が 2 階から 1 階に落ちている変わりに、変数が一つ増えている)
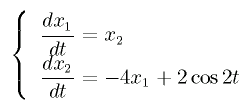
この形の微分方程式を一般化して以下のように書くことができる。
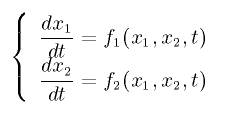
ここで、微分係数に対して以下の近似式を代入すると、
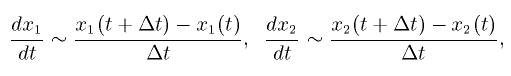
以下の式が得られる。これは、時刻 t における系の状態 (x1(t), x2(t)) から、時刻 t +Δt における系の状態
(x1(t+Δt), x2(t+Δt)) を求める式である。
この手法を Euler (オイラー) 法と呼ぶ。
この手続きを繰り返すことで、任意の時刻の系の状態を知ることができる。
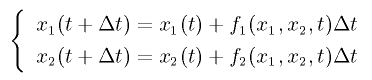
また、このように微分方程式を数値的に解くことを数値積分する、などと言う。
なお、上記の議論は本日の内容の背景の解説としてつけたのものであり、本講義では覚える必要はない。
では、実際に Euler 法で数値解を求めてみよう。
冒頭で述べたように、ここでは Visual Basic によるプログラミングを使わず、
Excel の機能のみを使って実現してみよう。
Excel の操作法としては新しいことは学ばないので、これはExcel 利用法の復習と思って欲しい。
(詳細は
Office 2013 の基礎
参照)
まず、準備として、第 1 列に以下のように「t」、「x1」、「x2」、「f1」、「f2」、「dt」と記述しよう。
この位置を合わせないと、以下の式も各自変更する必要があるので、図と同じ位置のセルを利用すること。

次に、時間 t、位置 x1、速度 x2 に初期値として 0 を記述し、数値積分の時間刻み dtに 0.01 を記述しよう。

次に、f1(x1, x2, t) = x2 を実現するため、セル D2 に
と記述しよう (上の枠つきの文字はコピー可能)。

次に、f2(x1, x2, t) = -4 x1 + 2 cos(2t) を実現するため、セル E2 に
と記述しよう。

次に、時刻 t を dt だけ増やすため、セル A3 に
と記述しよう。セル F2 を定数値として常に参照するため、絶対参照を用いていることに注意。

記述が終わると以下のように、セル A3 に 0.01 だけ進んだ時刻が表示される。
セル A3 が選択された状態で、セルの枠右下の■をマウスでつかみ、下方向へドラッグしてオートフィルしよう。

やや多めに、オートフィルで 1000 くらいコピーしておこう。
次に、x1(t+dt) = x1(t) + f1 (x1,x2,t)*dt を実現するため、
セル B3 に
と記述しよう。

同様に、x2(t+dt) = x2(t) + f2 (x1,x2,t)*dt を実現するため、
セル C3 に
と記述しよう。

セル D3 とセル E3 には、セル D2 とセル E2 に書いた式をコピーしよう。
2 つのセルをドラッグして選択し、右クリックでコピーし、

D3 セルを選択し、右クリックで貼り付ける。
すると、D3 と E3 に式がコピーされて値が表示される。

あとは、B3、C3、D3、E3 セルの式をオートフィルでコピーしていこう。
B3 から E3 までマウスでドラッグし、4 つのセルを選択する。
4 つのセルが選択された状態で、セルの枠右下の■をマウスでつかみ、下方向へドラッグしてオートフィルしよう。

A 列と同じ位置までコピーすればよいだろう。
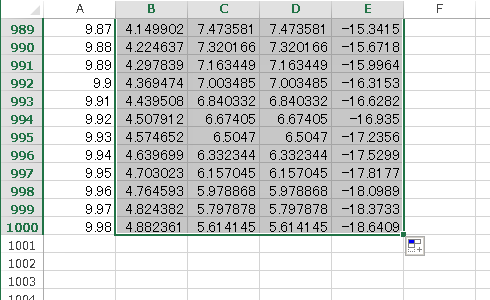
さて、以上で Euler 法による微分方程式の数値解のデータが準備できた。
このグラフを描いて確認してみよう。
以下のように、A 列と B 列を共に選択する。
「A」を一回クリックした後「Ctrl キーを押しながら、『B』をクリック」または 「A、B をマウスでドラッグ」で選択可能である。
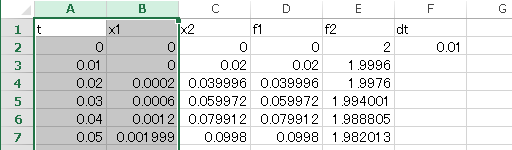
この状態で挿入タブから散布図を選択するのであった。
これにより、以下のようなグラフが描ける (これはまだラベルや軸名などを描いていない)。
これが微分方程式の数値解である。
以上で、Excel の機能のみを用いて微分方程式の数値解を Euler 法で求められることがわかった。
この数値解が、解析的な解とどれだけ異なっているかを調べてみよう。
この系の解析解は
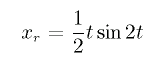
で書けることが知られている
(ただし、時刻 0 で位置と速度が 0 の場合)。
(なお、この解析解を得る方法を知るためには「微分方程式」を学ぶ必要がある)
数値解と解析解を同時にグラフに描いて、差を視覚化してみよう。
そのためには解析解のデータを準備する必要がある。
G 列に 以下のように解析解を用意しよう。書き込む式は
である。

そしてオートフィルで必要数のデータを揃える。
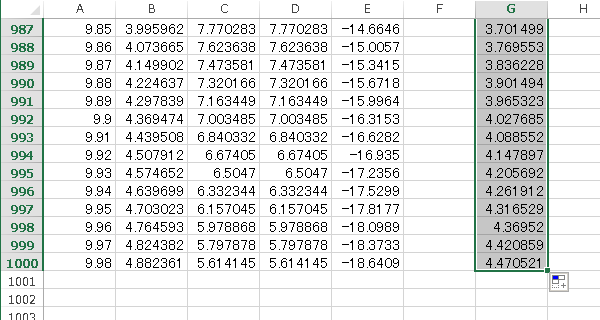
このデータのグラフを描くには、まず、A、B、G 列を同時に選択する。
そのためには、「A」を一回クリックした後、「Ctrl キーを押しながら、『B』、『G』を一回ずつクリック」すると良い。
この状態で挿入タブから散布図を選択する。
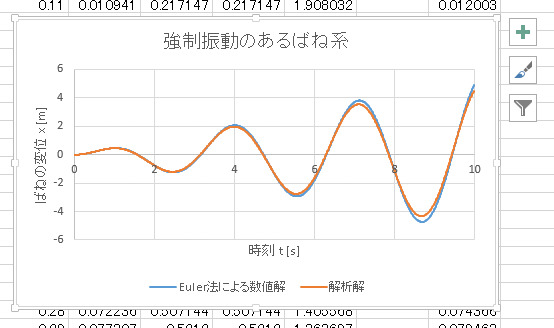
すると下図のようなグラフが得られる。
重要なことは、Euler 法による数値解と解析解の間に大きな誤差があることである。
これは Euler 法は (簡単ではあるが) 非常に性能の良くない数値積分法であるためである。
この誤差は次ページで学ぶ 4 次の Runge-Kutta 法を用いることでかなりの程度解消できる。
なお、グラフの凡例 (上の図で「Euler 法による数値解」や「解析解」と書かれた部分)
を変更するには、以下のように「元のデータ」から行う。
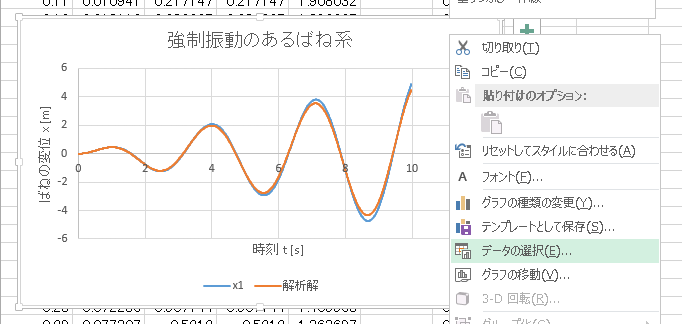
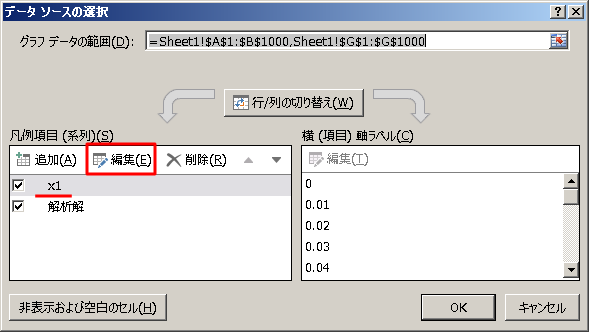
「データソースの選択」というダイアログが現れるので、
2たる系列のうち、編集したい方 (ここでは x1) をクリックして選択し、
「編集」ボタンを押す。
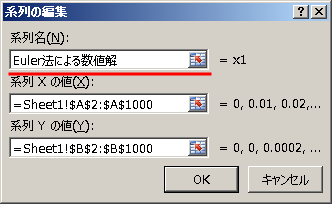
以下の「系列名」に表示したい内容を記述する。
←シートへの高速なアクセス/
微分方程式の数値的解法 (2) VBA + Excel→
Excel で学ぶ Visual Basic for Applications (VBA)に戻る