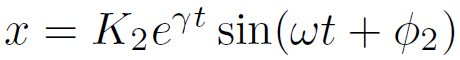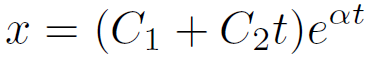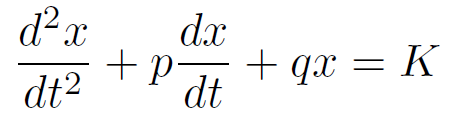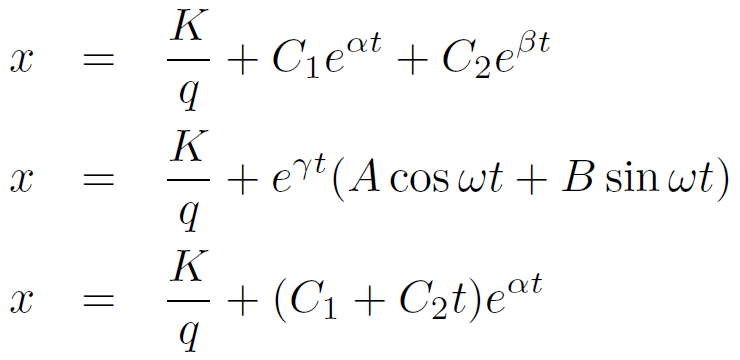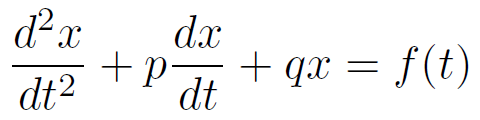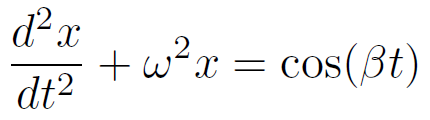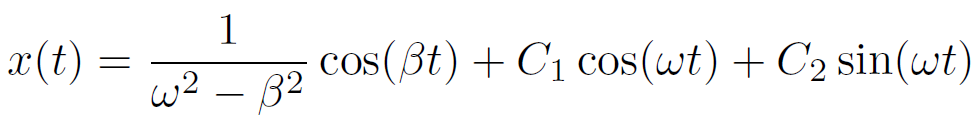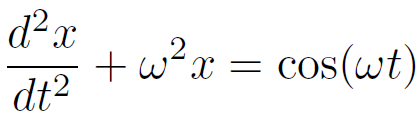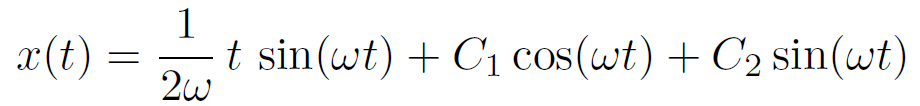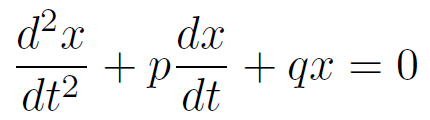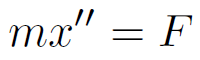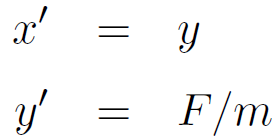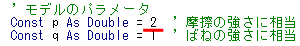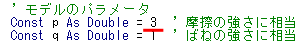第五回-02 2階定数係数線形微分方程式
今回は、2階定数係数線形微分方程式について学ぼう。
前回の1階定数係数線形微分方程式と同様、皆さんは既にこの内容を 1年生または2年生の「微分方程式」の講義で学んでいる。
それを「運動のシミュレーション」という観点からとらえなおすことになる。
1年生または2年生の「微分方程式」の講義で学んだ 2階定数係数線形微分方程式の内容を整理したのが以下の PDF ファイルである。
このファイルから結果だけを抜きだして以下で解説する。
典型的な2階定数係数線形微分方程式は次式で書ける。
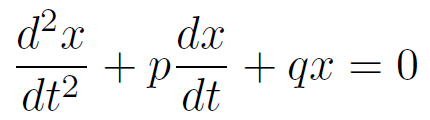
この微分方程式の解の性質は、下記の特性方程式の解により決まる。
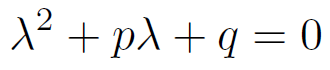
特性方程式は λ に関する二次方程式であるから、その判別式の値で解を分類できる。
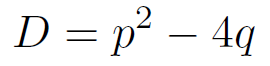
まず、D=p2 - 4q > 0 の場合、特性方程式は異なる二つの実数 α と β を持つ。それらを用いて解は以下のように書ける。
ただし、C1、C2は任意定数である。
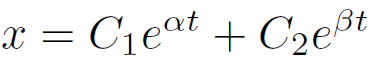
D=p2 - 4q < 0 の場合、特性方程式は異なる二つの複素数解 γ ± i ω を持つ。それらを用いて解は以下のように書ける。
ただし、A、B は任意定数である。
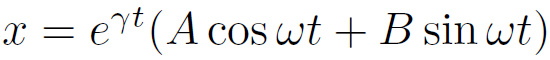
なお、上記の解は下記の2つの記法と数学的に等価である。
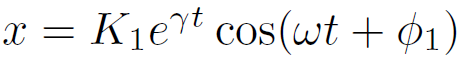 、
、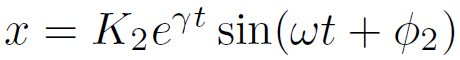
最後に、D=p2 - 4q = 0 の場合、特性方程式は重解 α を持つ。それを用いて解は以下のように書ける。
ただし、C1、C2は任意定数である。
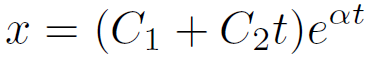
また、2階定数係数線形微分方程式に定数入力 K が加わった場合、
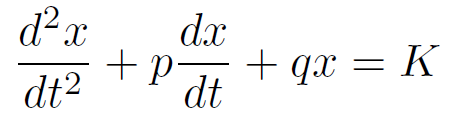
解は K=0 における解に K/q が加わったものとなる。
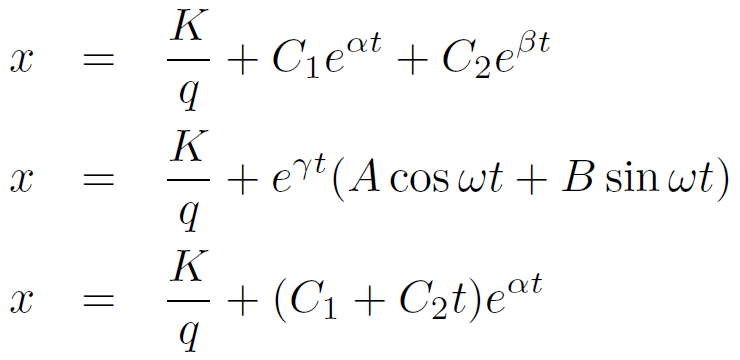
最後に、2階定数係数線形微分方程式に定数入力 f(t) が加わった場合を考える。
これは制御工学でお馴染みの形である。
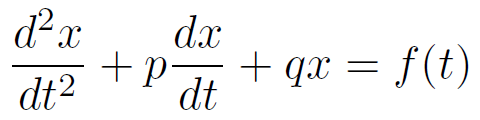
この場合は一般論で解説するのはやや面倒なので、例題とその解答を2つ提示する。
まずこちらの例題。角周波数 ω で振動する単振動系に、角周波数 β の振動入力が加わった場合。ただし、ω ≠ β とする。
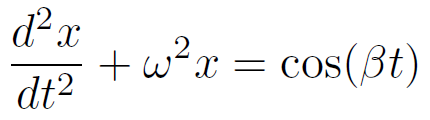
この場合の解は以下の通り。角周波数 ω と β の振動の和になっていることがわかる。
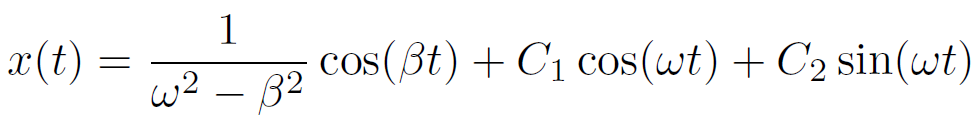
もう一つ例題はこちら。角周波数 ω で振動する単振動系に、同じく角周波数 ω の振動入力が加わった場合。
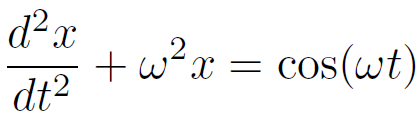
この場合の解はこちら。角周波数 ω の振動の和になっているが、第一項の振幅は t に比例しており、
時間とともに振幅が大きくなることがわかる。これは、システムのもつ固有周波数と外部からの入力の周波数が一致したときに起こる共鳴という現象である。
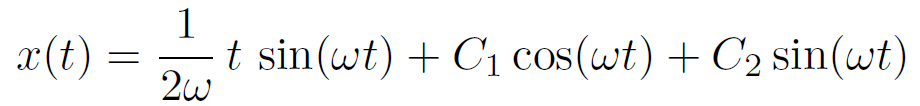
以上の内容をシミュレーションで体験してみよう。
2階定数係数線形微分方程式を数値的に解く Excel マクロを用いてシミュレーションを行ってみよう。
このマクロは次式の微分方程式のシミュレーションを行う。
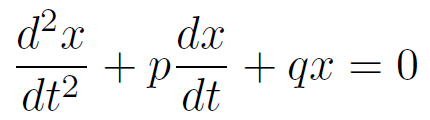
演習問題とそれに対する解答、という形式で解説を進める。
[演習問題1-1]
p=1, q=1 に対するシミュレーションを行え。
「開発」タブ→「Visual Basic」ボタンを押して現れるプログラムのうち、
今回編集するのは主に以下の部分である。

第二回のページで運動方程式
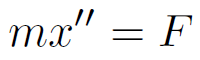
は、x の微分 (速度) を表す新たな変数 y を導入することで、以下のように書き直すことができることを学んだ。
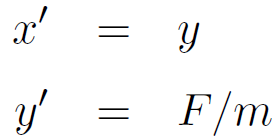
その形式でプログラムが書かれていることがわかるだろう。すなわち、
x'' = -px' -qx
が
x' = y
y' = -py -qx
と書け、それがプログラムとして以下のように表現される、ということである。
dxdt(0) = x(1)
dxdt(1) = -p*x(1) -q*x(0)
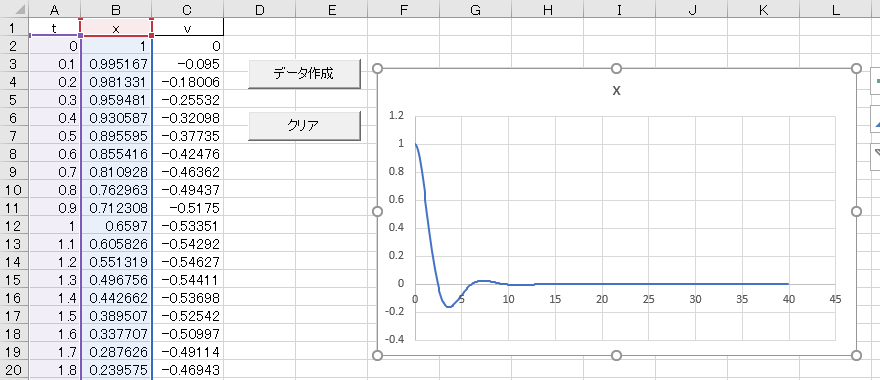
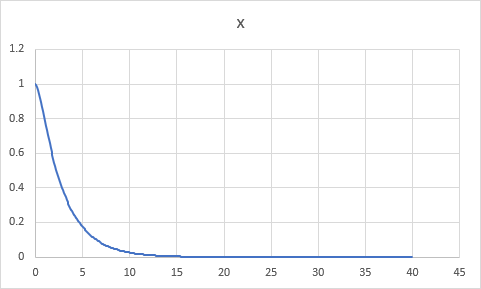
さて、プログラムを編集せずにそのまま「データ作成」ボタンをクリックし、A列とB列を散布図(直線)で描くと下図のようになる。
D = p2 - 4 q < 0 の場合なので、振動しながら減衰していることがわかる。
[演習問題1-2]
p=2, q=1 に対するシミュレーションを行え。
プログラムを下記のように編集し、「データ作成」ボタンをクリックしすれば良い。
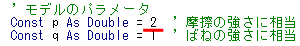
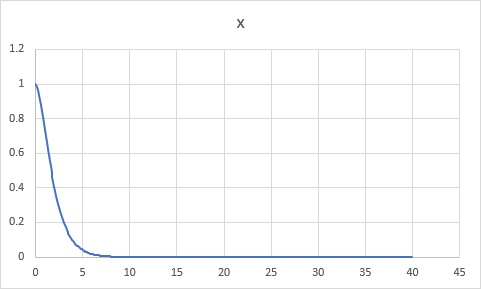
グラフは下図のように変化する。これは、判別式 D = p2 - 4 q = 0 の場合である。
[演習問題1-3]
p=3, q=1 に対するシミュレーションを行え。以上[演習問題1-1]~[演習問題1-3]のように結果が変化するのは何故か。
プログラムを下記のように編集し、「データ作成」ボタンをクリックしすれば良い。
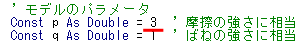
グラフは下図のように変化する。これは、判別式 D = p2 - 4 q > 0 の場合である。
結果が変化する理由は、既に述べてきたように判別式 D の正負が変化し、解の性質が変化したからである。
[演習問題2]
まずp=1, q=1 にセットする。K=10 なる定数 K を宣言し、微分方程式に q*K なる定数入力を加えてシミュレーションを行え。
下図のように K の定義を追加し、微分方程式に定数 q*K を追加しなければならない。p と q の値にも注意すること。

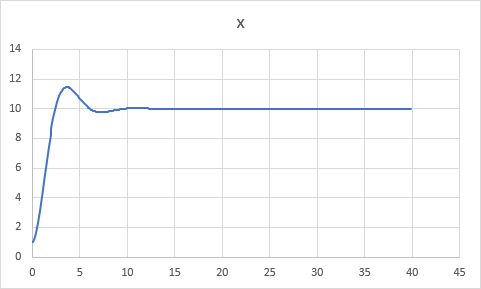
グラフは、下図のように目標値 K に向かって振動しながら収束する。
制御工学で良く見かけるグラフである。
[演習問題3-1]
まずp=0, q=1 にセットする。方程式に Cos(2*t) なる振動入力を加えた際のシミュレーションを行え。
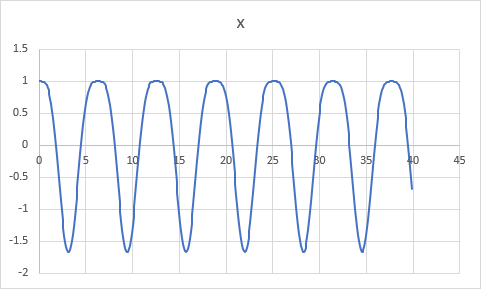
下図のように p を 0 にして Cos(2*t) を加える。

すると、下図のような振動が得られる。
[演習問題3-2]
p=0, q=1 にセットする。方程式に Cos(t) なる振動入力を加えた際のシミュレーションを行え。[演習問題3-1] と x の値が大きく異なるのは何故か。
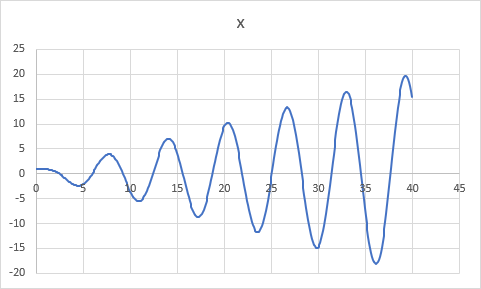
下図のように p を 0 にしたまま Cos(t) を加える。

すると、振幅が増大しながらの振動が見られる。
これは上で解説したように、システムの周波数と外部入力の周波数が一致したことによる共鳴という現象である。
課題→
Excel VBA で微分方程式をシミュレーションしように戻る
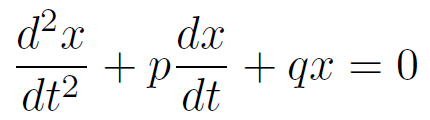
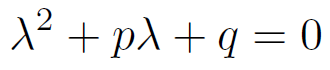
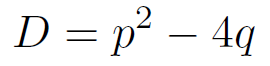
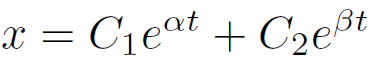
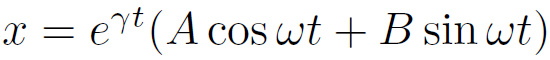
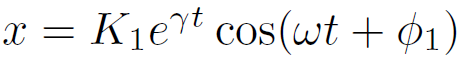 、
、