第二回-01 静力学と動力学/解析解と数値解
本講義の運動編で学ぶ内容を明確にするために、皆さんが学部で学んだ静力学と動力学について本ページで整理してみよう。
システムの状態を表すベクトルを x としたとき、静力学で取り扱うつりあいの式などは、以下の形で書ける。
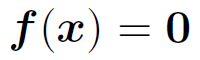
一方、システムの状態 x の時間変化を取り扱う動力学では、時間変化の法則を典型的には以下の形で記述する。
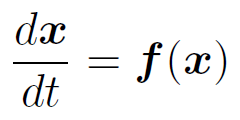
…と一気に書いてみたが、恐らく何の話だか良く分からない、という学生が多いのではないかと思う。
せっかくなので丁寧に解説してみよう。上の式中で、太字で表されている文字 x、f、0 は全てベクトルである。
すなわち、下図の1行目と2行目はベクトルの2種類の記法を表している。ゼロベクトルの存在も思い出しておこう。
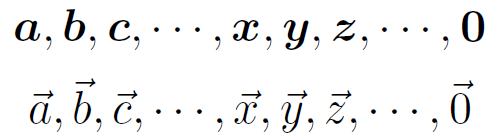
ベクトルであるから、x が n 次元ベクトルの場合、以下のように成分で書くことができる。
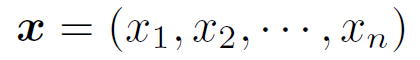
関数 f(x) が m 次元ベクトルである場合、以下のように m 個の関数を集めたベクトルを想像すればよい。
なお、f(x) の変数 x は、先程と同じく n 次元ベクトルとして成分で記述した。
つまり、n 個の変数を持つ多変数関数が m 個あるということである。
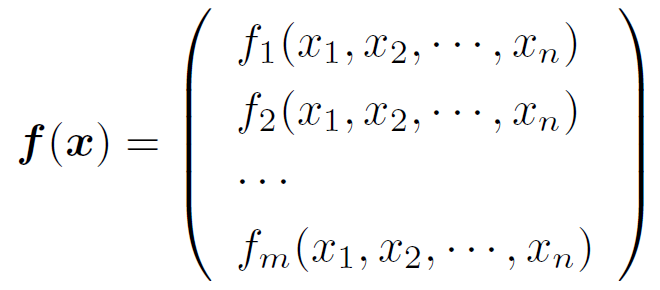
となると、静力学の基本式 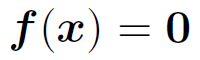 は以下のような連立方程式を表すことになる。
は以下のような連立方程式を表すことになる。
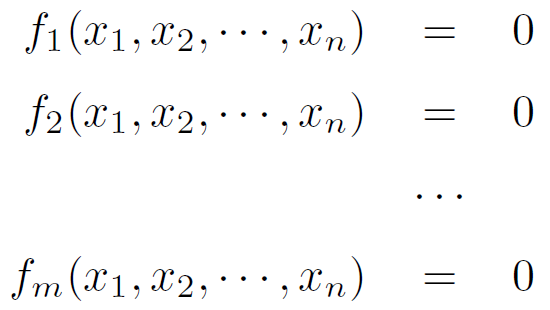
同様に、動力学の基本式 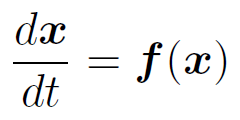 は以下のように連立した微分方程式を表すことになる。
は以下のように連立した微分方程式を表すことになる。
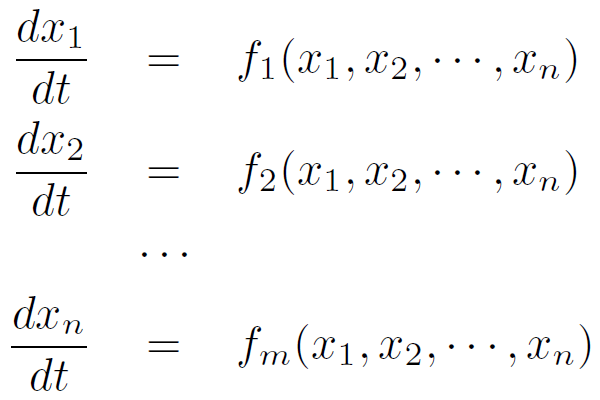
あまりピンと来ていない学生もいるかもしれないが、具体例を見れば難しい話はしていないことがわかるはずである。
まず、静力学の例として下図のおもりのつりあいを考えよう。
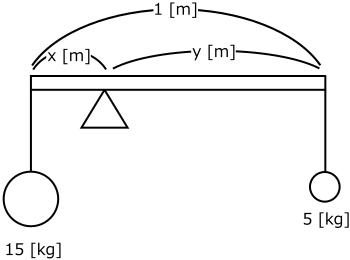
図中の長さ x, y に関して、棒の長さは 1 なのであるから x+y = 1 が成り立つ。
さらに、モーメントのつりあいに関して 15x = 5y が成り立つこともわかるだろう。
すなわち、整理すると次式が成り立つ。
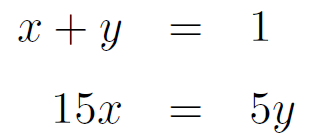
これは簡単な連立方程式なので以下のように簡単に解くことができる。
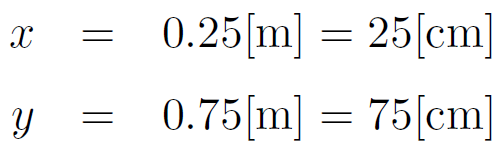
とは言え、ここで大事なのは上記の解答ではなく、つりあいの式が 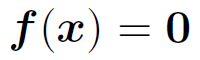 と書けることを確認することである。
と書けることを確認することである。
つりあいの式を整理すると以下のように書けることがわかる。
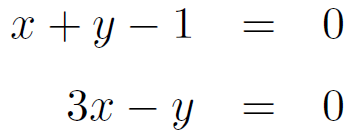
ここで、x = (x, y) と考えれば、上式は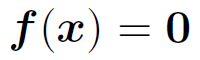 そのものであることがわかる。
そのものであることがわかる。
もう一つ、静力学の例を考えよう。
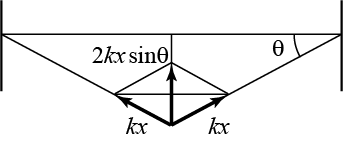
下図(左)のように壁の間に自然長 l、ばね定数 k のばねが2本渡されている。
ばねの中央に質量 m のおもりを静かにぶらさげると、ばねが延びて下図(右)のようにつりあいが実現される。
このときに成り立つつりあいの式を考えよう。
ばねののびを x、壁の鉛直方向とばねのなす角度を θ とする。
まず、直角三角形に着目すると、 l = (l+x) cos θ という図形に基づく式が得られる。
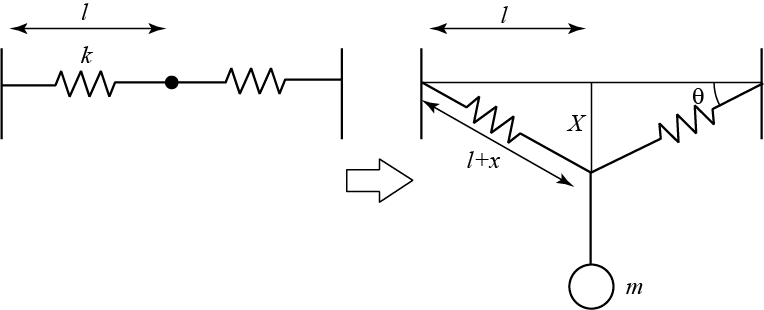
さらに、下図よりばねにより、おもりに対して鉛直上方向に 2kx sin θ の復元力が働くから、
mg = 2kx sin θ というつりあいの式が成り立つ。
まとめると、以下の2つの式が得られる。
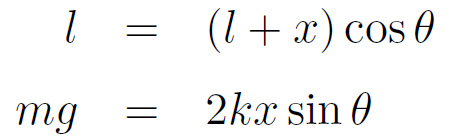
ここで、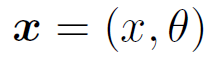 というベクトルを考えると、
というベクトルを考えると、
つりあいの式は
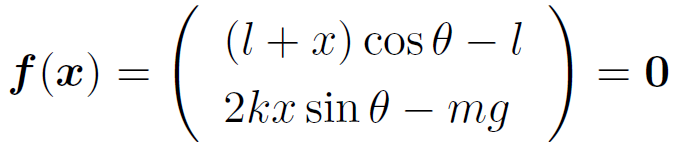
と書ける。やはり 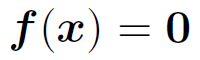 と書けることがわかるだろう。
と書けることがわかるだろう。
モーメントによるつりあいの例との違いは、こちらの例ではつりあいを満たす
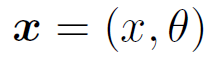 の値が
の値が
簡単には得られないということである。恐らく、コンピュータで近似的な値を求めるしかないだろう。
とはいえ、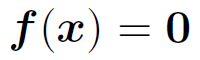 を満たす
を満たす 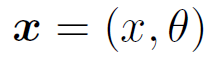 によりつりあいが実現されることは想像できるだろう。
によりつりあいが実現されることは想像できるだろう。
ひきつづき、壁に渡された2本のばねとおもりのシステムを考える。
先程は「静かにおもりをぶらさげる」と書いたので、つりあいの状態がすぐに実現されることが前提されている。
しかし、現実にはおもりから手を離したとき、ばねによりおもりがある程度振動してからつりあいが実現するだろう。
その運動の運動方程式は複雑なので今回は提示しないが、実際に運動方程式をたててシミュレーションを行うと、下図のような減衰振動を確認できる。
観測したのは、鉛直方向のおもりの位置 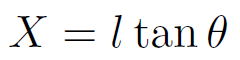 である (この X は上のばねの図にも記されている)。
である (この X は上のばねの図にも記されている)。
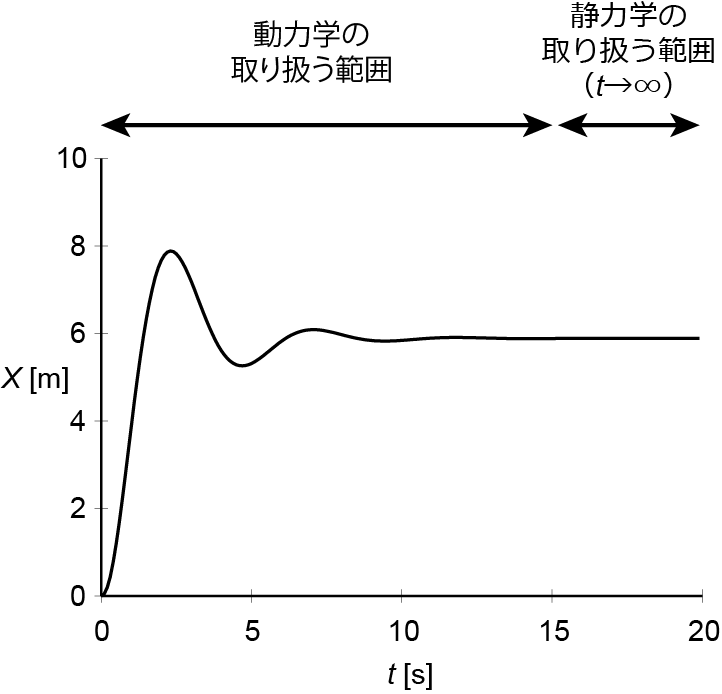
図中に示されているように、動力学とは物体が運動している過程を扱うものであり、静力学とは動力学で t→∞ の極限で実現された安定状態を扱うものである。
ただし、 t→∞ の極限でも安定状態に到達せず運動し続けるようなシステムは静力学の対象とはならないことに注意すること。
なお、これは本講義を通してそうなのだが、本講義ではシミュレーションの定数を「1 [kg]」や「1 [m]」などと雑に決めている。
そのため、「おもりの触れ幅が 6 [m]」とか「振動が収まるまで 10 [秒]」のようにやや非現実的な数値が登場することが多い。
それは 1 [kg] や 1 [m] のように簡単な数値を用いているためなので、あまり気にしないで欲しい。
さて、運動を記述する式として皆さんが知っているのは運動方程式である。
質点の一次元座標を x、働く力の総和を F としたとき、運動方程式は以下のように書けるのだった。
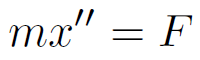
なお、x'' は x の時間での二階微分であり、加速度に相当するのだった。
この式は冒頭で紹介した動力学の基本式 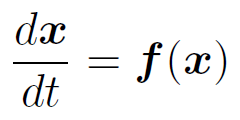 に従っていないように見える。
に従っていないように見える。
なぜなら、基本式には時間での一階微分しか含まれていないからである。
しかし、x の微分 (速度) を表す新たな変数 y を導入することで、上の運動方程式は以下のように書き直すことができる。
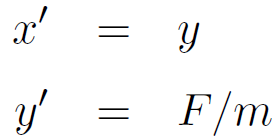
この微分方程式は 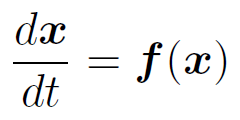 の形をしているので、運動方程式でも冒頭の議論が成り立つと言える。
の形をしているので、運動方程式でも冒頭の議論が成り立つと言える。
この変形は、運動方程式をコンピュータに解かせるときに必須となる重要なものである。
この式の導出は簡単であり、以下に示す通りである。

本ページの最後に、解析解と数値解という用語を紹介しよう。
解析解とは、運動方程式や微分方程式を解析的に解いた解のことを指す。
要するに、紙と鉛筆で問題を解くことで得られる解、ということである。理論解や厳密解などともいう。
皆さんがこれまで物理学や数学などで学んで来たのは、運動方程式や微分方程式の解析解を求める方法だったというわけである。
別の言い方をすれば、解析解を求めることのできるシステムを講義では取り扱うことが多い、とも言える。
一方で、コンピュータのシミュレーションにより求める解のことを数値解という。数値解を求めることを「数値的に解く」とも言う。
本講義では、運動方程式や微分方程式を数値的に解くことを皆さんに体験してもらうのだった。
運動方程式や微分方程式を書くことが出来る限り、数値解を得ることはほとんどの場合可能である。
そのため、数値解に触れた人は、手計算により得られる解析解のことを軽視するようになりがちである。
しかし、解析解には数値解にはない以下のようなメリットがあり、その重要性が薄れることはない。
- システムに含まれる様々なパラメータ (定数など) に対するシステムの応答を厳密に知ることができる
例えば、おもりとばねによる単振動において、おもりの質量 m やばね定数 k の値を変更したときに何が起こるかを厳密に知ることができる、ということである。
数値解では、定数を変えるごとに異なる数値解が得られるだけであり、定数と数値解の関係を明らかにできない。
本日の課題ではそれを体験してもらおうと思う。
運動方程式を数値的に解いてみよう→
Excel VBA で微分方程式をシミュレーションしように戻る
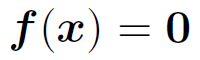
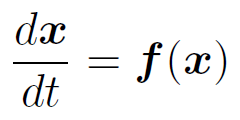
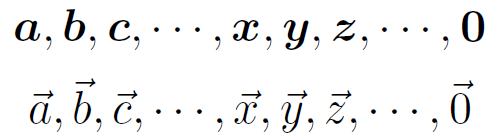
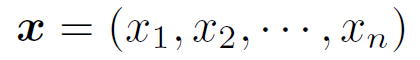
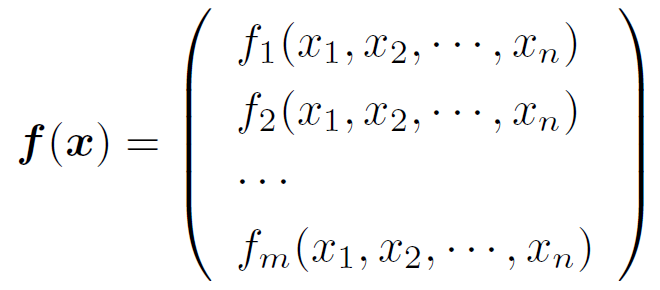
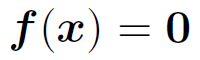 は以下のような連立方程式を表すことになる。
は以下のような連立方程式を表すことになる。
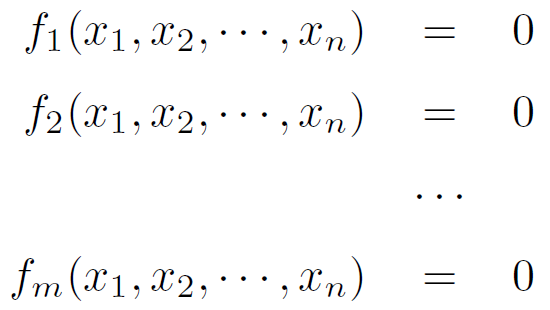
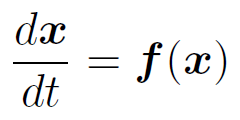 は以下のように連立した微分方程式を表すことになる。
は以下のように連立した微分方程式を表すことになる。
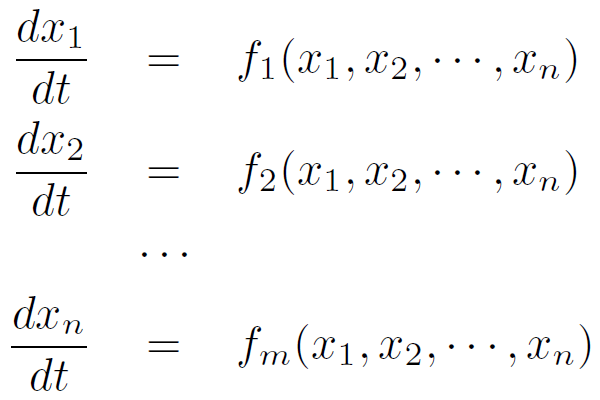

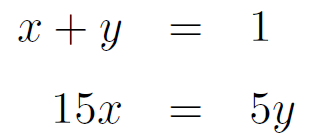
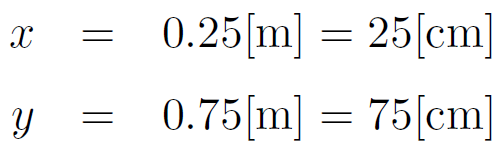
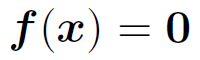 と書けることを確認することである。
と書けることを確認することである。
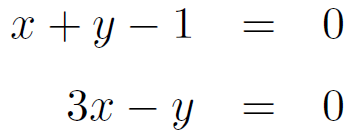
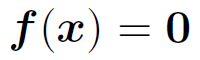 そのものであることがわかる。
そのものであることがわかる。


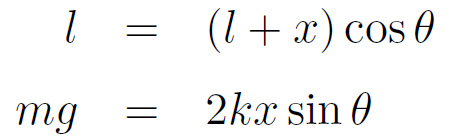
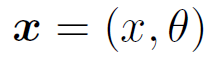 というベクトルを考えると、
というベクトルを考えると、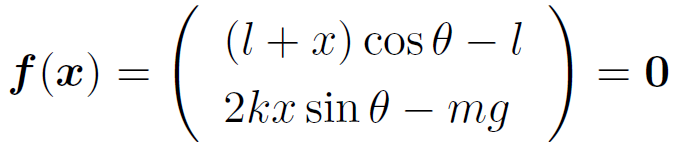
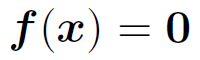 と書けることがわかるだろう。
と書けることがわかるだろう。
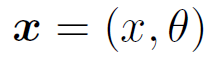 の値が
の値が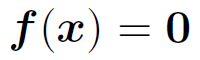 を満たす
を満たす 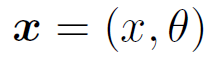 によりつりあいが実現されることは想像できるだろう。
によりつりあいが実現されることは想像できるだろう。
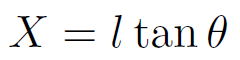 である (この X は上のばねの図にも記されている)。
である (この X は上のばねの図にも記されている)。

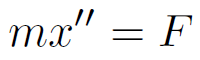
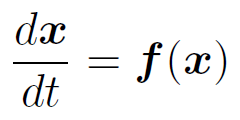 に従っていないように見える。
に従っていないように見える。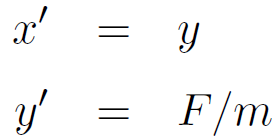
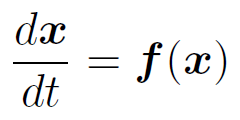 の形をしているので、運動方程式でも冒頭の議論が成り立つと言える。
の形をしているので、運動方程式でも冒頭の議論が成り立つと言える。