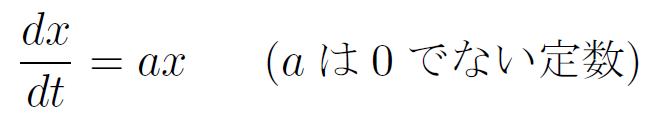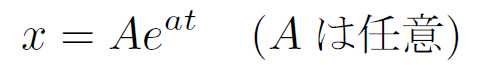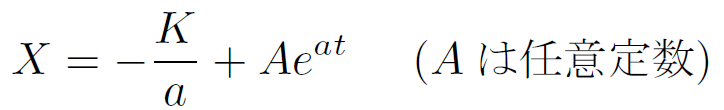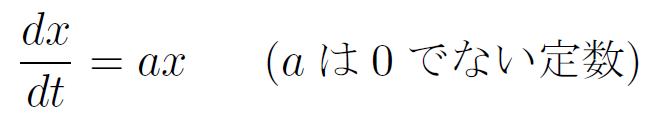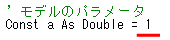第四回-01 1階定数係数線形微分方程式
今回は、前回学んだ線形微分方程式の一つである1階定数係数線形微分方程式について学ぼう。
皆さんは既にこの内容を 1年生または2年生の「微分方程式」の講義で学んでいるはずである。
それを「運動のシミュレーション」という観点からとらえなおすことになる。
1年生または2年生の「微分方程式」の講義で学んだ 1階定数係数線形微分方程式の内容を整理したのが以下の PDF ファイルである。
このファイルから結果だけを抜きだして以下で解説する。
1階定数係数線形微分方程式の典型例は以下の微分方程式である。
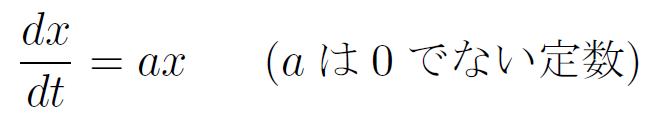
この解は以下で書ける。
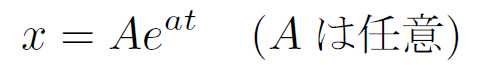
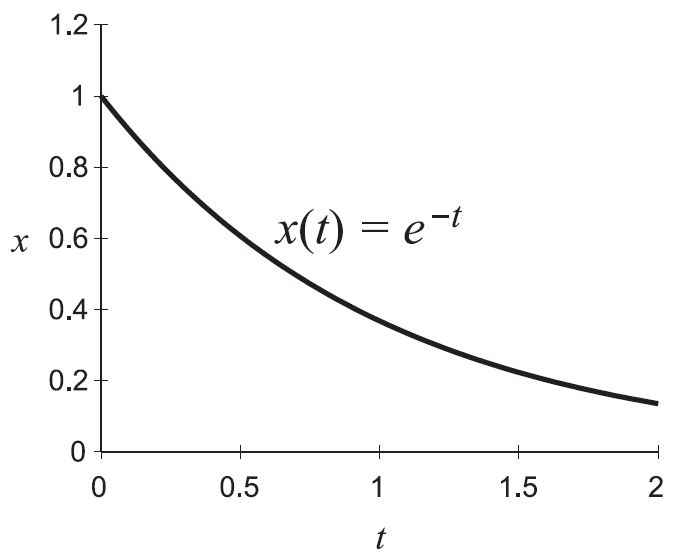
a<0 のときのグラフの典型的なイメージは以下である。A=1、a=-1 に対して描いた。
a<0 ではグラフは指数的に減衰するグラフとなる。このようなグラフは放射性物質の量が減衰する様子としても現れる。
このとき、a の絶対値の逆数 1/|a| は時間の次元を持ち、「その時間が経つと値が 1/e になる」という性質がある。
放射性物質の場合、 log2/|a| は「その時間が経つと値が 1/2 になる」という性質があり、半減期と呼ばれる。
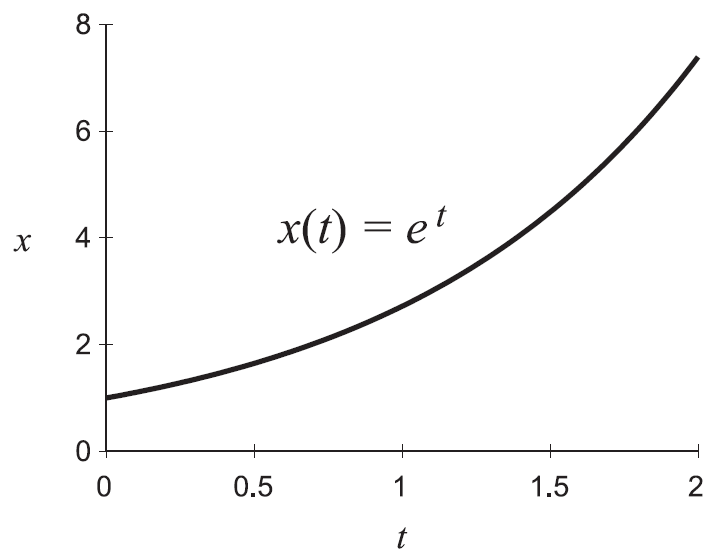
a>0 のときのグラフの典型的なイメージは以下である。A=1、a=1 に対して描いた。
このように値が∞に発散するのは、工学としては避けるべき状態である。
例えば、ばねが伸び切ってシステムが壊れる状態などに対応する。
または、感染症の初期の感染者数はこのように指数関数的に増加することが知られている。
皆さんも春からのニュースでご存知だろう。
また、次式のように微分方程式に定数項 K が加えたものもしばしば取り扱われる。

この場合の解は以下のようになる。
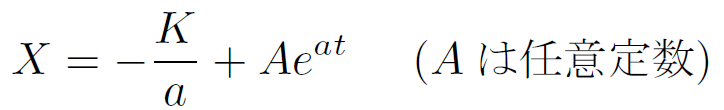
典型的なグラフは以下のようになる。K=1、a=-1、A=-1に対して描いた。収束先は -K/a = 1 となる。
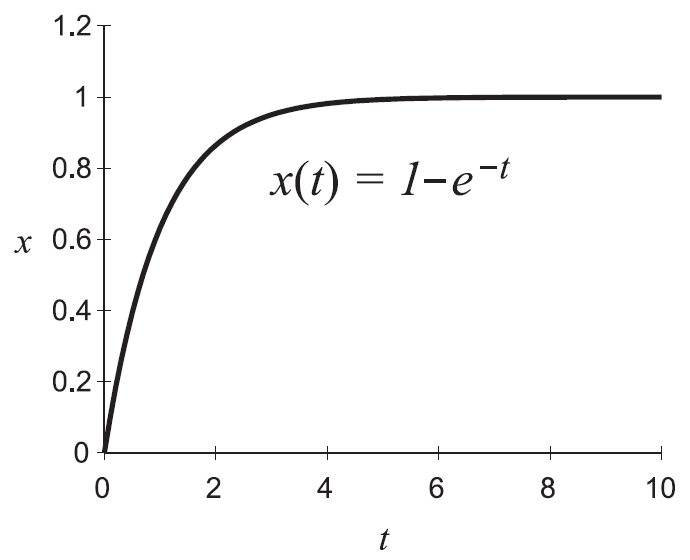
なお、収束先が -K/a となるのは、もともとの微分方程式からも類推できる。
値が収束した後、グラフは水平となって傾きがゼロとなるのだから、dx/dt = 0 となるはずである。
それをもともとの微分方程式

に代入すると、次式が得られる。これを解いて x = -K/a が得られるのである。
0 = ax + K
1階定数係数線形微分方程式を数値的に解く Excel マクロを用いてシミュレーションを行ってみよう。
このマクロは次式の微分方程式のシミュレーションを行う。
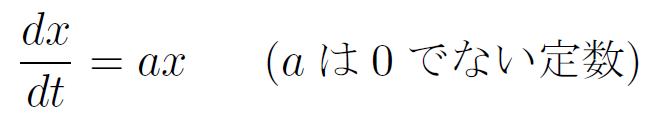
演習問題とそれに対する解答、という形式で解説を進める。
[演習問題1]
まずはそのままシミュレーションを行って散布図でグラフ化し、a=-1 で結果が 0 に収束することを確認せよ。
「開発」タブ→「Visual Basic」ボタンを押して現れるプログラムのうち、
今回編集するのは主に以下の部分である。

下記の行が、定数 a = -1 を定めていること、
Const a As Double = -1
下記の行が、微分方程式 dx/dt = ax を表していることに注意。
dxdt(0) = a * x(0)
「データ作成」ボタンをクリックし、A列とB列を散布図(直線)で表示すると以下のようになる。
指数的減衰のグラフが見られるのは、 a=-1 <0 だからである。
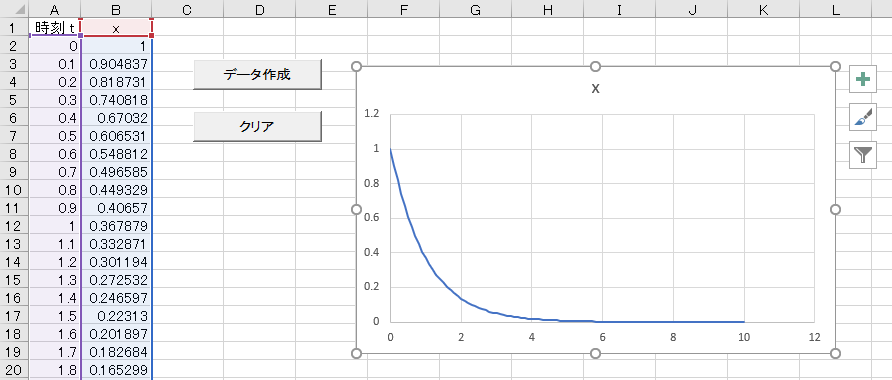
[演習問題2]
次に定数 a の値を -1 から 1 に変えてシミュレーションを行え。結果が (1) と大きく変わった理由は何か。
a を設定している行を以下のように変更してから「データ作成」ボタンをクリックすれば良い。
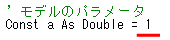
グラフは以下のように変化する。先程とグラフが大きく変わった理由は、定数 a の値が a<0 から a>0 に変化したからである。
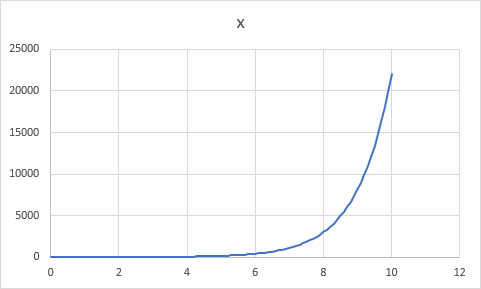
[演習問題3]
再び定数 a の値を -1 に戻そう。さらに定数 K を K=10 として定義し、微分方程式の右辺に定数項 -a*K を加えよう。
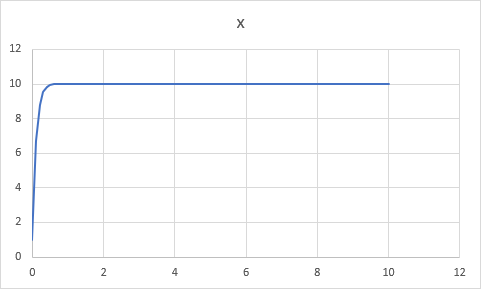
シミュレーションの結果、x は K の値に収束することを確認せよ。
プログラムを下記のように変更する。

K を定義する行を一行追加する必要があるが、a の行をコピーして流用すれば比較的容易であろう。
定数は K そのものではなく -a*K を与えることにした。これは、結果を分かりやすくするためである。
具体的には、収束先が K そのものになる。
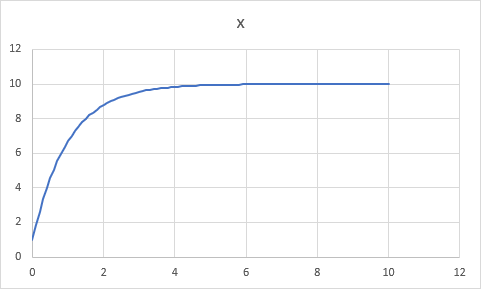
[演習問題4]
[演習問題3]の設定のまま、a の値を -10 に変更せよ。収束の速さはどう変わるか。また、それはなぜか。
変更点は下記の通り。

グラフは下記のように速く変化する。その理由は、上で書いたように、
1/|a| が時間の次元を持ち、その値で変化の速さを決めるからである。
すなわち、|a| が大きくなれば時間に相当する 1/|a| は短くなる、すなわち変化が速くなるのである。
ローパスフィルター→
Excel VBA で微分方程式をシミュレーションしように戻る