 |
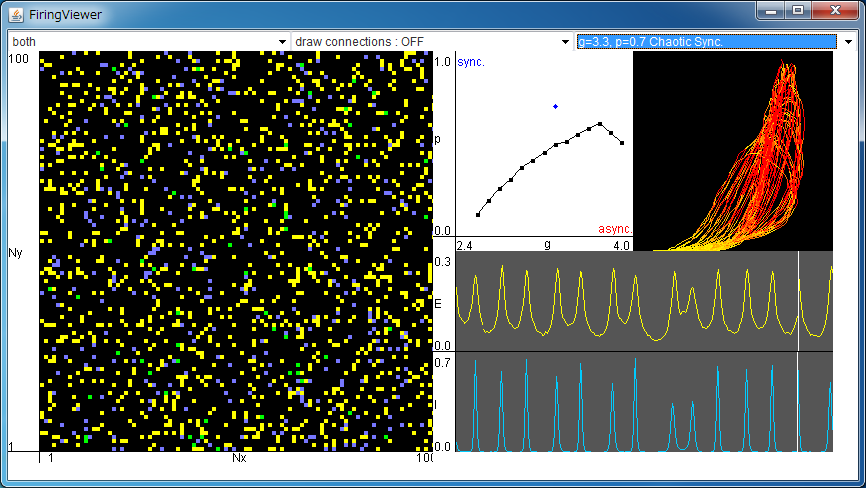
Firing of neurons
|
On the 100x100 two-dimensional grid,
an excitatory neuron (E) and an inhibitory neuron (I) are placed.
The firings of excitatory neurons and inhibitory neurons are shown by
yellow dots and blue dots, respectively.
The firings of both neurons are shown by
green dots.
|
 |
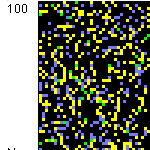
The plane of the connection strength g between E&I ensembles and rewiring probability p
|
By regulating the values of the connection strength g between E&I ensembles and the rewiring probability p,
you can observe asynchronous firing (async.) and
synchronous firing (sync.).
In this simulator, you can choose the dynamics
from two asynchronous dynamics and two synchronous dynamics,
which are periodic synchronization and chaotic synchronization,
by clicking this (g,p) plane or by using the choice on upper right.
|
 |
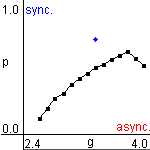
(JE,JI)
|
Flows of the ensemble-averaged firing rates JE and JI for excitatory and inhibitory ensemble are shown in the (JE,JI) plane.
Asynchronous firing shows an equilibrium, and synchronous firing
shows time-varying dynamics, such as a limit cycle and a chaotic attractor.
|
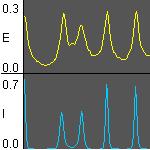 |
Temporal changes in JE(t) and JI(t)
|
Temporal changes in JE(t) and JI(t) are shown.
Yellow and blue denote
the excitatory and inhibitory ensemble, respectively.
|