 |
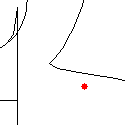
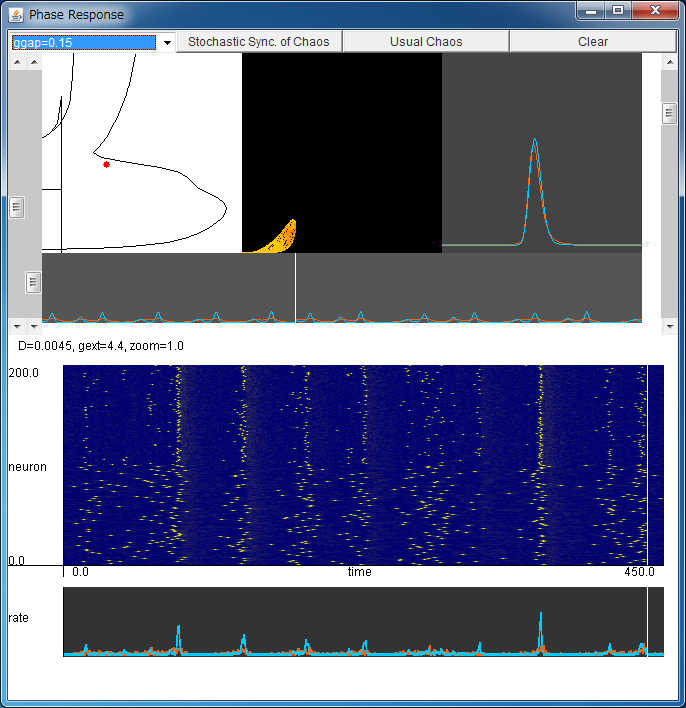
Parameter Setting
|
By clicking your mouse in this field, you can change the noise intensity D (horizontal axis) and the external coupling strength gext=gEI=gIE (vertical axis).
Synchronized firings and chaotic synchronized firings are observed depending on the values of the parameters.
The values of the parameters can be regulated using two left scroll bars.
|
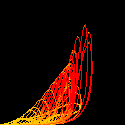 |
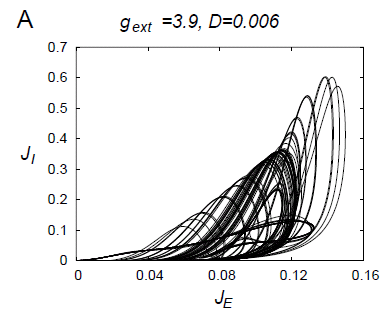
(JE,JI)
|
Flows of the ensemble-averaged firing rates JE and JI for
excitatory and inhibitory ensemble are shown in the (JE,JI) plane.
Various forms of chaotic attractors would be observed.
You can zoom in/out using the right scroll bar.
|
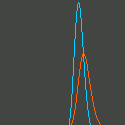 |
(nE,nI)
|
Temporal changes in the probability densities nE and nI of
excitatory and inhibitory ensemble, are shown.
Red and blue denote
the excitatory and inhibitory ensemble, respectively.
|
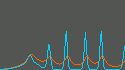 |
Temporal changes in JE(t) and JI(t).
|
Temporal changes in JE(t) and JI(t) are shown.
Red and blue denote
the excitatory and inhibitory ensemble, respectively.
These flows correspond to the simulation with NE=NI=100 below.
|
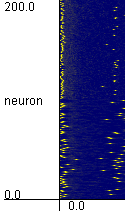 |
Simulation with NE=NI=100
|
Firing times of the neurons in the system with NE=NI=100 are plotted.
The neurons in the range from 1 to 100 are excitatory,
and the neurons in the range from 101 to 200 are inhibitory neurons.
|
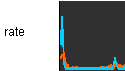 |
The ensemble-averaged firing rates of the network with
NE=NI=100
|
Temporal changes in the ensemble-averaged firing rates of the network with NE=NI=100.
Red and blue denote
the excitatory and inhibitory ensemble, respectively.
They correspond to the above JE(t) and JI(t)
which are obtained in the limit of large numbers.
|






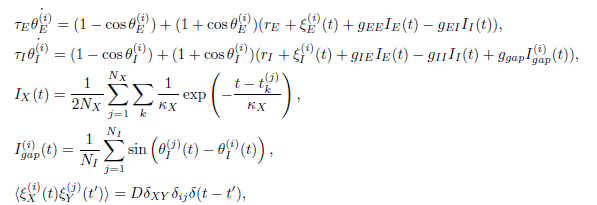
 The connections IX(t) model the chemical synapses,
and they give post-synaptic potentials
only when the presynaptic neuron fires.
The connections IX(t) model the chemical synapses,
and they give post-synaptic potentials
only when the presynaptic neuron fires.
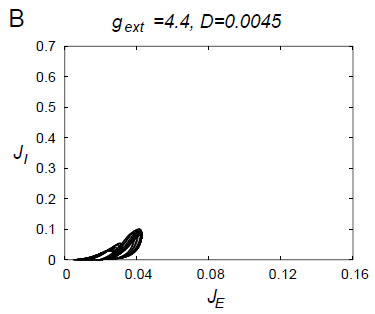 By the analysis with the Fokker-Planck equation,
when the values of the parameters are appropriately chosen,
this network shows a low-dimensional chaotic attractor
as shown in the above figure.
By the analysis with the Fokker-Planck equation,
when the values of the parameters are appropriately chosen,
this network shows a low-dimensional chaotic attractor
as shown in the above figure.
