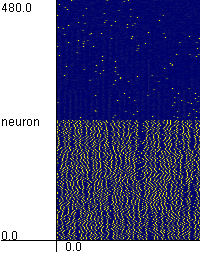
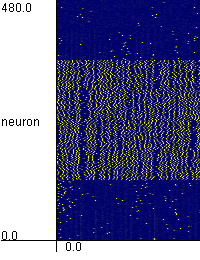
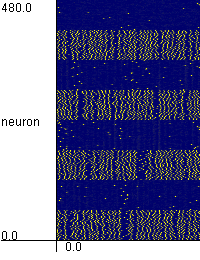
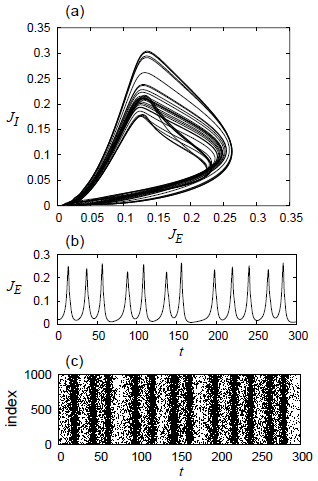
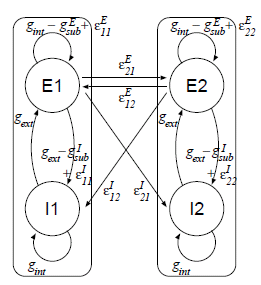
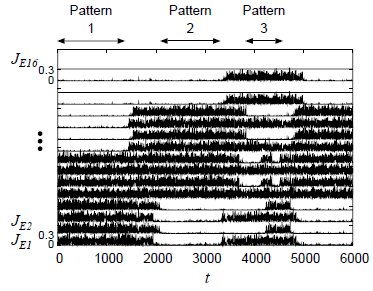
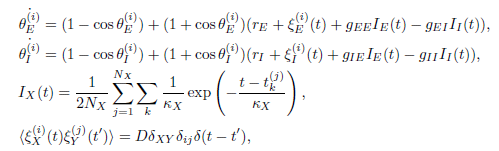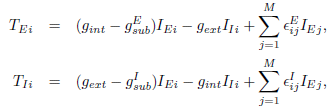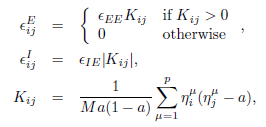Chaotic Pattern Transitions in Pulse Neural Networks



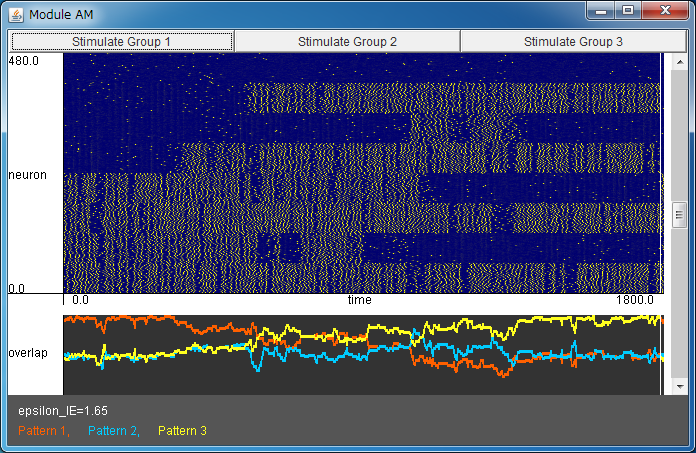
After downloading pnnam.jar, please execute it by double-clicking, or typing "java -jar pnnam.jar".

When the pattern transitions do not take place, please press "Stimulate Group x" button,
and then the neurons which store pattern x are stimulated. The pattern transitions are often induced by that.

If the above application does not start, please install OpenJDK from adoptium.net.

Stored Patterns
Pattern 1
Pattern 2
Pattern 3


In this research, chaotic associative memory is realized using a pulse neural network, although it is often realized using the conventional analog-valued neurons.

Let us consider a pulse neural network composed of excitatory pulse neurons and inhibitory pulse neurons, and this network is called one module of network in the followings.

The neurons are globally connected with chemical synapses whose post-synaptic potential has an exponential waveform, and noise is added to each neuron.


In the limit of large number of neurons, the ensemble-averaged dynamics of a module of network has a chaotic attractor as shown in left figure (a).

Left figure (c) shows the raster plot of the firings of 1000 excitatory neurons in a module, and it is observed that the times at which synchronous firings take place fluctuate chaotically. Left figures (a) and (b) show the result of analysis obtained in the limit of large number of neurons.

By regarding this "one module" as "one element" of associative memory, a model of associative memory is constructed with a multiple modules of pulse neural networks. Right figure shows a schematic diagram of the connections between two modules.
The connection matrix is determined by the modified Hebbian rule written as





By regulating the values of parameters, chaotic associative memory is realized in this pulse neural network as shown in the left figure.

In this applet, a module of network is composed of 60 excitatory and 60 inhibitory neurons, and 3 patterns are stored in 8 modules of networks.
The yellow points show the firings of excitatory neurons, and the drawing of the states of inhibitory neurons is omitted.

Because the number of neurons is small, noise as well as chaos induces pattern transitions, and the patterns are sometimes destroyed by the finite size effect.

When the pattern transitions do not take place, please press "Stimulate Group x" button, and then the neurons which store pattern x are stimulated.
The pattern transitions are often induced by that.

The inhibitory connection strength can be regulated with the right vertical bar.
The patterns tend to be stable when the inhibitory connection strength is large.

This page is based on the following papers.
<< Rewiring-induced Synchronization and Chaos in Pulse-coupled Neural Networks / Stochastic Resonance >>

Introduction to Chaos and Nonlinear Dynamics