Lorenz Attractor
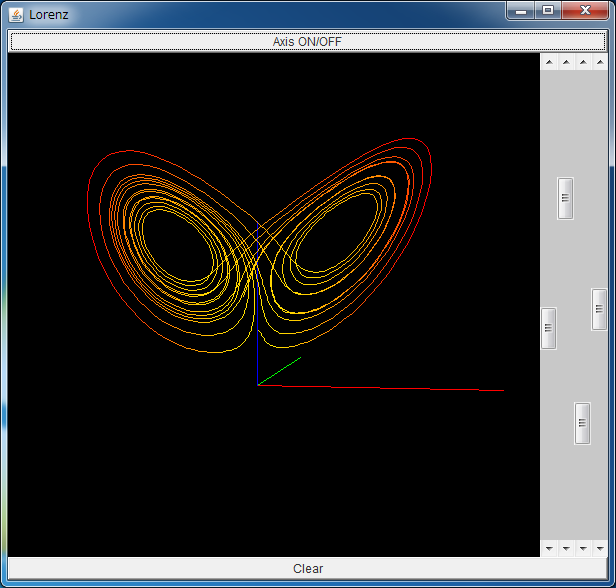
After downloading lorenz.jar, please execute it by double-clicking, or typing "java -jar lorenz.jar".
If the above application does not start, please install OpenJDK from adoptium.net.

| dx/dt= | -10x | +10y | |
| dy/dt= | 28x | -y | -xz |
| dz/dt= | -8/3z | +xy. |