Rössler Attractor

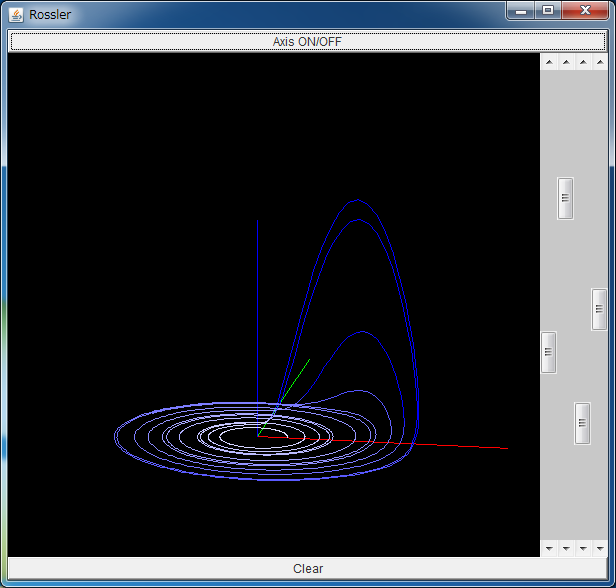
After downloading rossler.jar, please execute it by double-clicking, or typing "java -jar rossler.jar".

If the above application does not start, please install OpenJDK from adoptium.net.

The Rössler attractor is generated by the differential equation written by

dx/dt=	-y	-z
dy/dt=	x	+ay
dz/dt=	b	-cz	+xz.

The parameters are fixed as a=0.15, b=0.20, and c=10.0.
The point governed by the above equation typically converges to a strange attractor.

Similarly to the Lorenz attractor, the Rössler attractor is often introduced as a chaotic attractor in the three dimensional space. In an article on Rössler attractor in Scholarpedia, Dr. Rössler himself talks about the days when he created the above equation.

After that, he has continued the research on chaos theory, such as the hyperchaos where there are more than two positive Lyapunov spectra, and endophysics which incorporates the effect of internal observers into physics, chemistry, and biology.

In this page, you can observe the Lorenz attractor from various view angles.

The red, green, and blue lines denote the x, y, and z axes, respectively.
You can change the view with the three left bars, and you can change the zoom with the most right bar.

<< Lorenz Attractor / Attractor of Duffing Equation >>

Introduction to Chaos and Nonlinear Dynamics