[Excel で VBA] プロシージャの再帰的呼び出し

数学的な関数を作成する手法を第九回に Function プロシージャとして学んだ。

本ページではこの Function プロシージャを自分自身から呼び出す再帰的呼び出しについて学ぶ。

プロシージャの再帰的呼び出し

フィボナッチ数列と呼ばれる数列をプログラミングすることを考えよう。 数学的には、フィボナッチ数列は以下のの漸化式から生成される。

an = an-1 + an-2
a1 = 1
a2 = 1


このとき、

a3 は a2=1 と a1=1 を用いて a3 = 2、
a4 は a3=2 と a2=1 を用いて a4 = 3、
a5 は a4=3 と a3=2 を用いて a5 = 5、
…


のように次々と数列 an が生成される。

このとき、整数 n が与えられた時に値 an を返すような Function プロシージャを考えるのがここでの目標である。

理論上は上の手続き、すなわち「a1、a2、a3… と順番に求めて行き、an に達したら処理を止める」
という手法で計算できることはわかるであろう。
それをプログラムとして実現するためには、For 文による繰り返し、 If 文による条件分岐などを
駆使すればできそうだということも想像がつくであろう。
(ここまでの知識でできるので試してみると良い。)

しかし、じつは上の様に漸化式で書ける数列は「再帰的呼び出し」の考え方を使えば 簡単にプログラムできる。

では、フィボナッチ数列を求める以下のプログラムを記述して試してみよう。
(Visual Basic Editor の起動方法は「第一回：プログラムを書き始めるまでの準備」参照)





Function プロシージャ fib(n) が実際にフィボナッチ数列を求める部分であり、 上の解説では an に相当する。
そして、an-1 + an-2 に対応する部分は fib(n-1)+fib(n-2) のように自分自身を呼び出すことで実現している。

このとき、fib(5) の計算がどのように進むかのイメージ図を以下に挙げる。



ただ単に自分自身を呼び出すだけではプロシージャ呼び出しが無限に続くだけであるが、
n=1 と n=2 の時の値 (fib(1) と fib(2)) を 1 と指定していることで、再帰的呼び出しが終了する点も図から読み取って欲しい。

また、図では fib(5) が図のように「一気に」計算されるように見えるかもしれないが、
この計算も通常のプログラムと同様に「一ステップずつ」進む。
やや冗長になるが、この計算がどのように一ステップずつ進むのかを以下に記しておこう。 

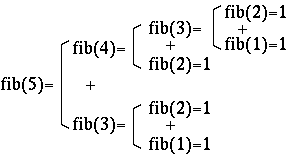
fib(5) の計算には fib(4) と fib(3) が必要
↓
fib(4) の計算には fib(3) と fib(2) が必要
↓
fib(3) の計算には fib(2) と fib(1) が必要
↓
fib(2)=1
↓
fib(1)=1
↓
よって fib(3)=fib(2)+fib(1)=2
↓
fib(2)=1
↓
よって fib(4) = fib(3) + fib(2) = 3
↓
fib(3) の計算には fib(2) と fib(1) が必要
↓
fib(2)=1
↓
fib(1)=1
↓
よって fib(3)=fib(2)+fib(1)=2
↓
よって fib(5)=fib(4)+fib(3)=5





←引数を変更するプロシージャ／ シートへのアクセス→

Excel で学ぶ Visual Basic for Applications (VBA)に戻る