第二回-03 コンピュータ上の数値の表現 (1) 0 を含む正の整数の2進数による表現

しばしば言われるように、コンピュータではデータやプログラムなどは全て 0/1 からなる2進数で表現される。
今回の講義ではこの2進数を理解することを目指そう。

ここで理解することを目指すのは以下の 2 つである。 0 を含む正の整数のみならばそれほど難しくはないが、負の整数も対象に入れると注意しなければならないことが増える。
課題ではそこを理解したかどうかを問うことになるだろう。

10進数の理解

2進数について学ぶ前に、我々が普段使っている10進数について確認しておこう。
10進数の特徴としてまず以下が挙げられる。 この10種類の数字を並べて数を表現するわけだが、その並んだ数の意味を、
4桁の数字 1234 を例に解説すると、以下のようになる。 

1234 = 1×103  + 2×102 + 3×101 + 4×100
     = 1×1000 + 2×100 + 3×10  + 4×1

念のため補足しておくが、100 = 1 であるので注意すること。

上で示されているのは、1234と四つ並んだ数字はそれぞれ「10 の冪乗(べきじょう)の何倍か」を表したものである、ということである。
すなわち、1234 は10 の冪乗の整数倍の和から構成されることを上の計算は示している。

ここでは例として4桁の10進数を取り上げたが、何桁の10進数であっても同じ考え方ができることは想像できるだろう。

ちなみに、正の整数を表現した4桁以下 (1～3桁も含む) の10進数では何通りの数値が表現でき、最大値はいくつかわかるだろうか？
10進数なので皆さん問題なく答えられるはずである。すなわち、以下の通りである。 対象の数値が2進数だった場合にこの問いに答えられるかどうか、頭に留めながら次に進もう。

0を含む正の整数を表現する2進数

次に、10進数の知識に基づき、0を含む正の整数を表現する2進数について学ぶ。
まず、2進数について10進数と同様に表現するならば、以下の特徴があるといえる。 すなわち、2進数は 0000 や 0101 や 1101 などのように 0 と 1 からなる数である、ということである。
なお、例として 0000、0101、および 1101 と 4 桁の2進数を3つ提示したが、2進数の桁数のことをビット数、1桁のことをビットという。
すなわち、例示されたのは 4 ビットの 2進数が3つということである。

また、10 進数では左端の桁の 0 は省略して書くが、 (1234 とは書くが、01234 とは書かない、など)
ビット数を指定した2進数では左端の桁の0は省略しないことが多い (すなわち4ビットにおける 0000、0101 のように)。

さて、0を含む正の整数が2進数で表現されている場合、その意味は 10 進数と同様に考えれば良い。
例えば、2進数の 1101 が表す正の整数は、以下で計算される。 

1101 = 1×23 + 1×22 + 0×21 + 1×20
     = 1×8  + 1×4  + 0×2  + 1×1
     = 13

こちらでも念のため補足しておくが、20 = 1 であるので注意すること。

上の計算より、2進数の 1101 は 10進数の13に対応することがわかる。

ここでは4桁、すなわち4ビットの例を提示したが、10進数と同様に何桁の (何ビットの) 2進数だろうと、
上と同様の計算により該当する10進数を計算することができる。

ここで 10 進数のときと同様に、4ビット の 2 進数で0を含む正の整数を表現したとき、
何通りの数値が表現でき、最大値はいくつかを考えてみよう。

解き方には様々な方法があるが、最小値と最大値を求めるのが最も簡単であろう。
最小値は全てのビットが 0 である 0000、すなわち 10 進数の 0 である。
最大値は全てのビットが 1 である 1111、これは以下で計算されるように 10 進数の 15 である。 

1111 = 1×23 + 1×22 + 1×21 + 1×20
     = 1×8  + 1×4  + 1×2  + 1×1
     = 15

すなわち、4 ビット の 2 進数で0を含む正の整数を表現したとき、表現できる数は以下の通りである。 ちなみに、上の「16通り」は、高校数学の数学Aで学んだように、
「独立に 0 か 1 をとることができる桁が 4 つある」わけなので、24 = 16 とも計算できる。

さて、ここまでの知識を整理すると、下図のように、「0を含む正の整数を表現した10進数」と「0を含む正の整数を表現した2進数」について学び、
「0を含む正の整数を表現した2進数」を「0を含む正の整数を表現した10進数」に変換する方法を学んだ、ということになる。



この図を見ると、逆向きの変換(「0を含む正の整数を表現した10進数」→「0を含む正の整数を表現した2進数」)も欲しくなる。次にそれを学ぼう。

0を含む正の整数である10進数から2進数への変換

それでは、「0を含む正の整数を表現した10進数」を「0を含む正の整数を表現した2進数」に変換する方法を学ぶ。
それにより、例えば 10 進数の 1234 を 2 進数に変換することができるようになる。

そのためには、2進数の考え方で学んだように、1234 を 2 の冪乗の和で表現できれば良いことがわかるだろう。
それを機械的に実行する方法を解説したのが以下である。

以下のように 1234 を 2 で割り、その商を下に、余りを「…」の右に書く。
すなわち、商が 617、余りが 0 である。
同様に、617 を 2 で割り、その商を下に、余りを「…」の右に書く。
これを商が 1 になるまで繰り返す。



これが完了したら、上図右側のように、最後の商と余りを下から順に並べてゆく。
すなわち 「100 1101 0010」が「1234」の 2 進数での表現である。
なお、このように数字が見やすくなるよう、下の桁から 4 桁ごとに空白を入れることがしばしばある。

得られた結果は、 

1234 = 100 1101 0010 = 210 + 27 + 26 + 24 + 21

を表している。気になる学生は計算して確かめてみると良い。

以上で、下図のように「0を含む正の整数を表現した10進数」と「0を含む正の整数を表現した2進数」とを相互に変換できるようになった。



2進数の表を書けるようになろう

ここまでで、「冪乗の数の和で表現する」という定義に基づき、
「0を含む正の整数を表現した10進数」と「0を含む正の整数を表現した2進数」を相互に変換できるようになった。

しかし、定義に基づいた考え方だけでは、2 進数を直観的に理解できないかもしれない。
そこで、2 進数にもう少し馴染むために、2 進数の表を書けるようになってみよう。

何ができて欲しいかを明確にするために、4 ビットの 2 進数の表を提示すると以下のようになる。



この表を皆さんが書く場合、当然 10 進数の部分は書けるだろう。
また、上で触れたように、4ビットの2進数で0を含む正の整数を表現する場合、最小値が 0000、最大値が 1111 というのも良いであろう。

問題は、2進数のうち、0000 と 1111 の間の部分がどのようなルールで書かれているかである。

そのルールを知るためには、2進数の数の足し算について学ぶ必要がある。
とは言え、それほど難しいことはない。1 ビットの2進数の足し算である下記の３つの計算を理解すれば良い。 注意が必要なのは、３つめの計算だけであろう。2 進数で 1 と 1 を加算すると、桁上がりが発生し、10 となるのである。
2進数の 10 は 10進数の 2 であることに注意すること。
なお、2進数の 10 は「じゅう」と読まずに「いちぜろ」と読むことにも注意すること。

以上を知れば、下図のように、2進数の上の欄の値に 1 を足して表を埋めて行けば良いことがわかる。



もう少し詳しく書けば、以下のように 2進数の足し算を繰り返して表を作成する、ということである。 

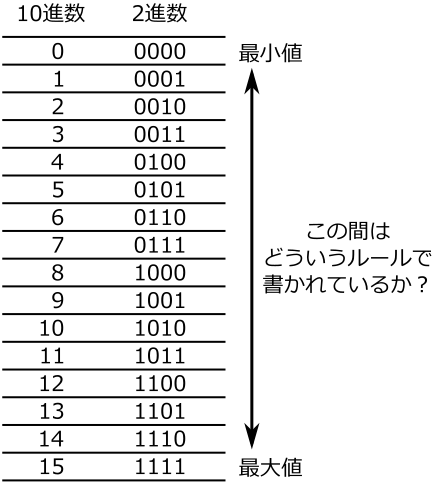
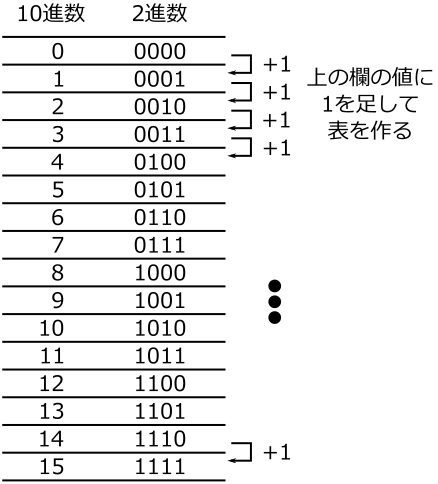
   0000   ←2進数の0
+)    1
-------
   0001   ←2進数の1

   0001   ←2進数の1
+)    1
-------
   0010   ←2進数の2

   0010   ←2進数の2
+)    1
-------
   0011   ←2進数の3

   0011   ←2進数の3
+)    1
-------
   0100   ←2進数の4

一度 0000 から 1111 までの表をこの方法で作成してみると、2進数の感覚がつかめるであろう。


←第二回-02 プログラムを実行するとはどういうことか ／ 第二回-04 コンピュータ上の数値の表現 (2) 負の数を含む整数の2進数による表現～2の補数表現→

非情報系学生のための C/C++ 入門に戻る