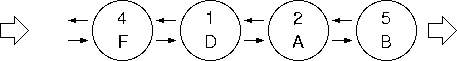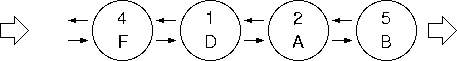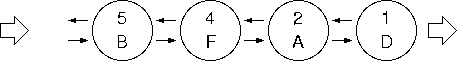第五回-04 : 二分木の概念

課題で見るように、リスト構造は queue クラスに関係が深い。
一方、ここからは「二分木」と呼ばれる構造をもとに priority queue (優先順位付きキュー) を作成することを目指す。

ただし、時間の都合上、ソースコードの全てを理解するのは難しいと思うので、 まずはこちらの提示した部分を理解することを目指して欲しい。

リストの復習と問題点

二分木はある優先順位に従ってデータを格納する際に役にたつ。

まずは具体例で解説する。「学籍番号と成績 (A～F)の組」というデータを考えよう。
学籍番号は 1 から始まる整数とし、成績は char 型の変数で表現できる。

今、テスト (やレポート) の採点結果に従って、「5 番: B」、「2 番: A」、「1 番: D」、「4 番: F」…というデータが次々と入って来るとしよう。
(始めから学籍番号順にテストやレポートを回収すれば良いのだが、そう都合良く事が運ぶことはほとんどない)

リスト (またはキュー) にこのデータを格納してゆくことを考えると、



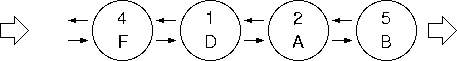
のようになるだろう (ただし、一つの Node が学籍番号と成績の両方を格納できるよう拡張する必要がある)。
見て分かるように、これでは全員の成績データがバラバラに並んでおり、データ管理が大変である。 下の図のように、始めから学籍番号順に格納されるようになっていれば便利であろう。



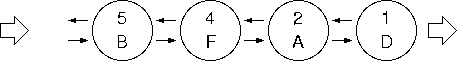
第五回-03の最後でも触れたように、 リスト構造は配列と違って、値の挿入が簡単にできるので、
成績結果を挿入する際に、既に存在している学籍番号をスキャンし、 新しいデータを挿入すべき場所を探して挿入すればよい。

しかし、 この方法は挿入する場所の探索に平均 N のオーダーの時間がかかるので効率が悪い (N は既に格納されているデータの数)。
このように、ある優先順位 (ここでは学籍番号順) にデータを格納したいときは リストよりも以下で述べる二分木の構造が効率が良く、広く使われている。

二分木

二分木とは、一つの Node の下に左右に二つの Node を取ることが出来るような構造をいう。
まずは、「5 番: B」→「2 番: A」→「1 番: D」→「4 番: F」→「8 番: A」→「9 番: C」データを順に二分木に格納した結果を先に図示しよう。



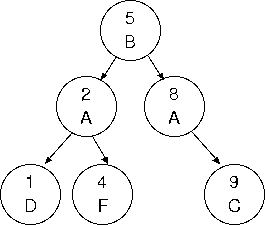
Node が二つに枝分かれし、木のような構造を成していることがわかる。
この二分木は、以下のルールで生成された (自分でも描いて確認してみよ)
このように作成された木は、学籍番号を優先順位として、順序づけられてデータが格納されていると言える。

では、このように格納された成績データを学籍番号の小さい方から取り出すにはどうしたらよいだろうか。
図で考えると簡単で、下の図のように学籍番号が小さい方からデータを辿ってゆく ポインタのようなものがあれば良い。



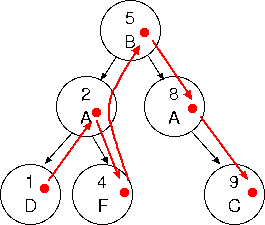
C++ の標準テンプレートライブラリ (STL) にはこれに似た振舞いをする ものが存在し、イテレータ (反復子) と呼ばれている。
我々もこのイテレータに似たものをプログラムに組込むことにする。 (ただし、記述は難しいのでこちらで提示する)

さて、リストに push と pop 機能をつけると queue になることは課題で確認するが、 二分木に push と pop 機能をつければ priority queue (優先順位つきキュー) になる。
「5 番: B」→「2 番: A」→「1 番: D」→「4 番: F」→「8 番: A」→「9 番: C」 の順で priority queue にデータを push すると、
「1 番: D」→「2 番: A」→「4 番: F」→「5 番: B」→「8 番: A」→「9 番: C」 のように学籍番号順でデータが pop される。

←第五回-03 : リストの実装 ／ 第五回-05 : 二分木の実装と利用→

第五回トップページへ

クラスから入る C++ へ