Standard Map



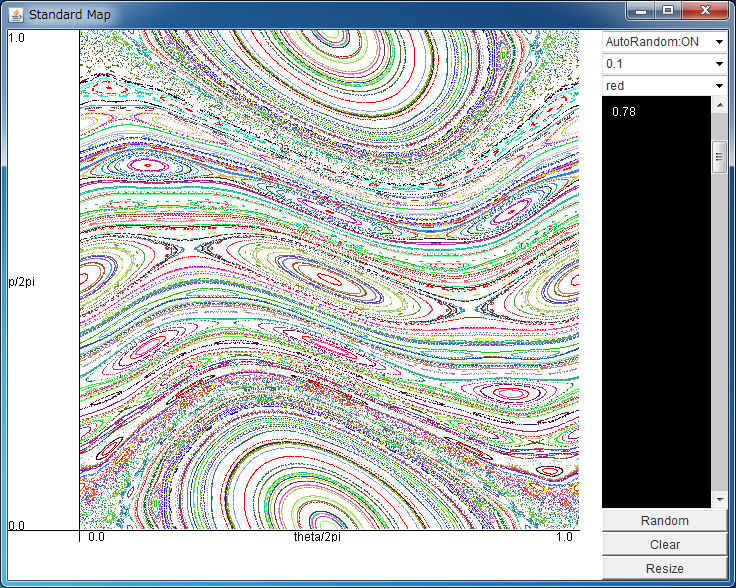
After downloading standard.jar, please execute it by double-clicking, or typing "java -jar standard.jar".

By clicking your mouse, you can set the initial value of a time evolution.
By dragging your mouse, you can expand the field.

If the above application does not start, please install OpenJDK from adoptium.net.

In this page, we treat a two dimensional map known as the standard map, written as

θn+1 = θn + pn modulo 2π,
pn+1=pn+K sin(θn+1) modulo 2π.

The volume on the phase space (in this case, the area of two dimensional space) is conserved because the determinant of Jacobian matrix of this map is one.
Therefore, there is no strange attractor in this system unlike Hénon map. (Shrinking of the volume is required for existence of strange attractor.)

Like this map, the system in which the volume in phase space is conserved is called conservative system, and it is distinguished from dissipative system in which the volume shrinks. In the conservative system, "destruction of invariant tori", "generation of islands of tori", and "chaotic sea" are typically observed.

Please see the number of the upper right of the simulator. This number (0.1) is the value of parameter K and it means the strength of non-linearity. The nonlinearity of the value 0.1 is not so strong.
Then please push the "Random" button. The 70 random initial values are chosen, and following sequences are plotted on the field. You will see many curves cross the space from left to right. They are the invariant tori, which are the surviver of the tori that existed for K=0. On the other hand, you will see many ellipses on the upper and lower of the field. They are the islands of tori which were generated with the increase of K.
The theorem which explains the destruction of invariant tori and the generation of the islands of tori is called Poincaré-Birkhoff's theorem.

The larger K becomes, the more invariant tori are destroyed and the more islands of tori are generated. The last invariant torus which remains under large K is called the golden torus.

If you choose the much larger K, few curves are observed and the time evolution like sands appears, which is called "chaotic sea".
<< Extensible Pendulum / Harper Map >>

Introduction to Chaos and Nonlinear Dynamics