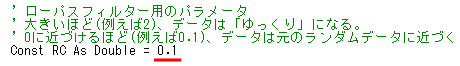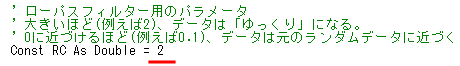第四回-02 ローパスフィルター
1階定数係数線形微分方程式は、工学においてしばしば登場する「ローパスフィルター」と関係が深い。
シミュレーションで体験してみよう。
ローパスフィルターも、学部時代の微分方程式の知識で理解できる。
そのように解説した資料が以下のPDF である。
エッセンスだけを述べよう。以下の電気回路を考え、E(t) が入力、V(t) が出力と考える。
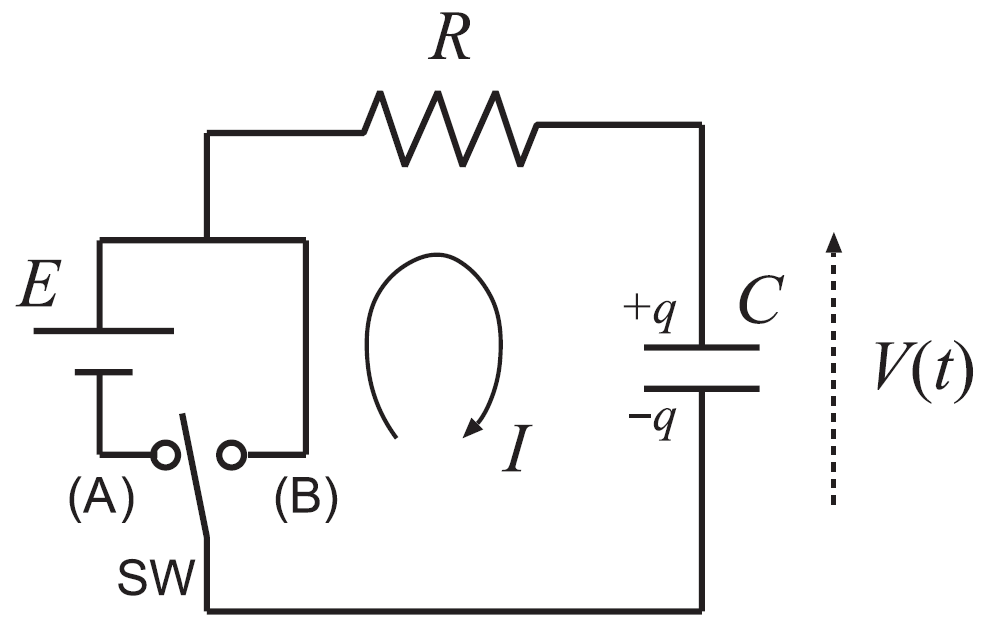
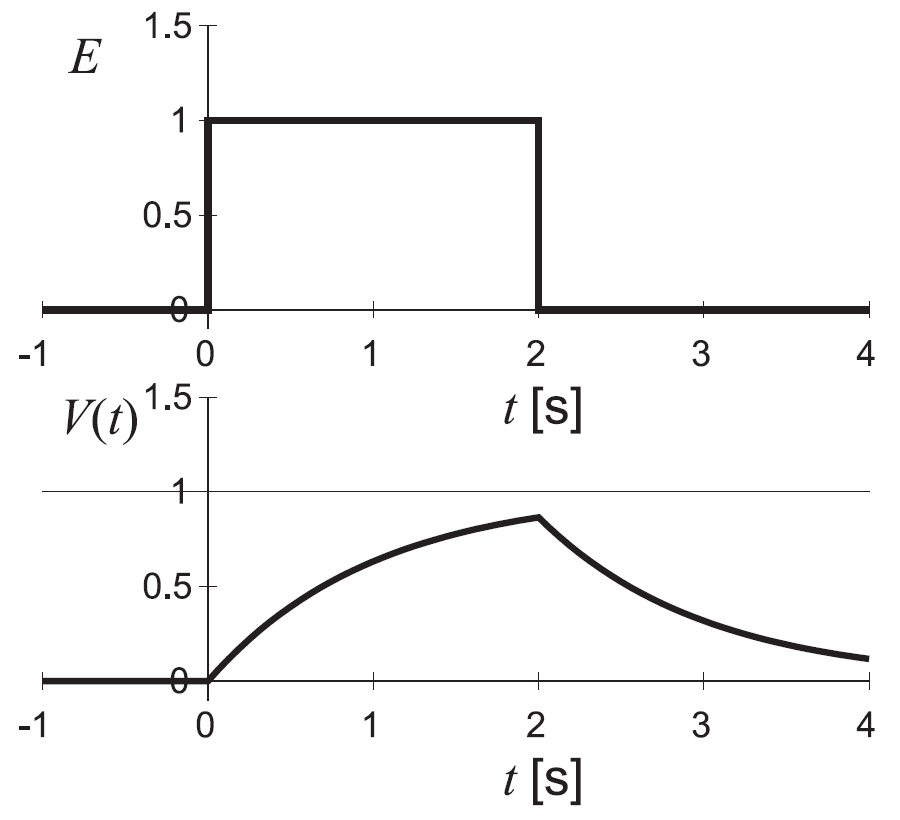
E(t) を 0 → 1 → 0 と素早く変化させると、出力 V(t) はその速い変化に追随できず、ゆっくりと変化する。
これを言い替えると、「入力の高周波成分が取り除かれ、低周波成分のみが出力に現れる」となる。
この性質をもつものをローパスフィルターという。
それでは、ローパスフィルターのシミュレーションを行うマクロをダウンロードしよう。
このマクロは、入力として「0/1の切り替え」と「ノイズ」の二種類を選択できる。
こちらも解答つきの演習を行う、と言う形式で解説する。
[演習問題1]
まずはそのままシミュレーションを行って散布図でグラフ化し「入力」が「出力」で滑らかになることを確認せよ。
入力は「0/1の切り替え」と「ノイズ」の両方に対してシミュレーションを行い、それぞれの入力に対するローパスフィルタの効果を確認せよ。
なお、「ノイズ」は「データ作成」ボタンをクリックするたびにノイズの系列が変化する。
0/1の切り替えの場合はこちら。
なお、これまでと異なりA列~C列の3列分のデータをプロットすること。
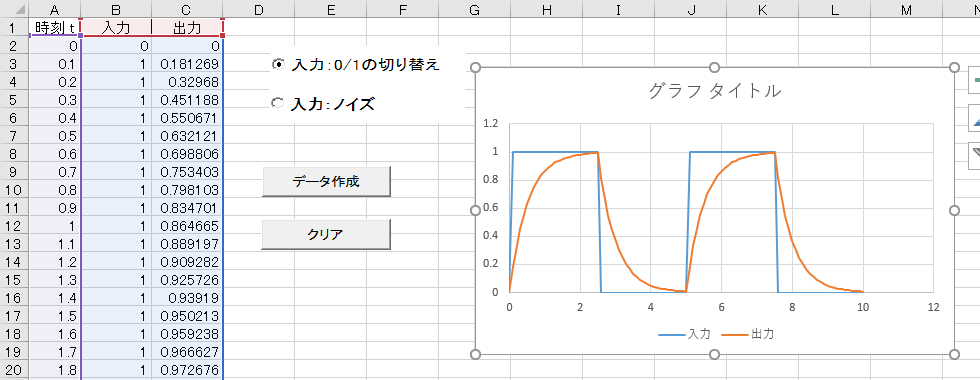
ノイズの場合はこちら。ノイズは毎回ランダムにデータが作られるので、人によりグラフは異なる。
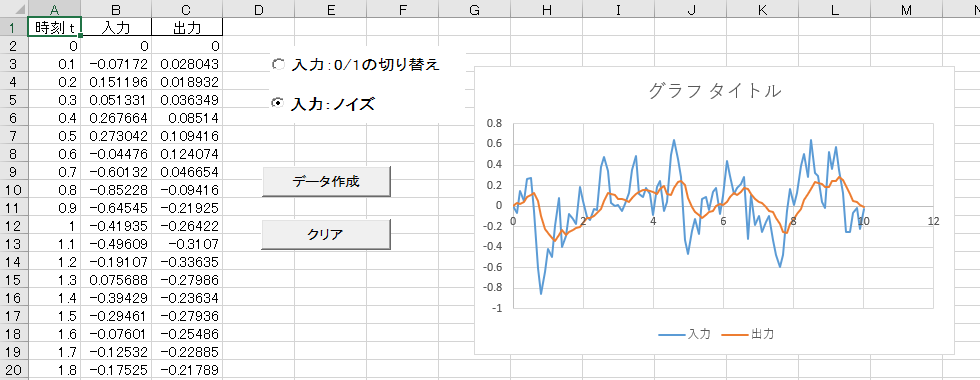
どちらも、「入力が出力で滑らかになる」ことがイメージできたのではないだろうか。
[演習問題2]
次に定数 RC の値を 0.5 から 0.1 に変えてシミュレーションを行え。ローパスフィルターの性質はどう変わるか。RCはローパスフィルターの時定数と呼ばれる。
変更箇所のは以下の通りである。
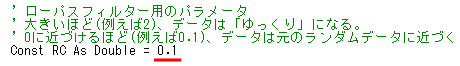
なお、今回のように定数の値を書き換えたら、シート上で「入力:0/1の切り替え」をクリックしなおして欲しい。
0/1の切り替えの場合はこちら。時定数、すなわち時間が短くなると言うことは、速く変化するということである。
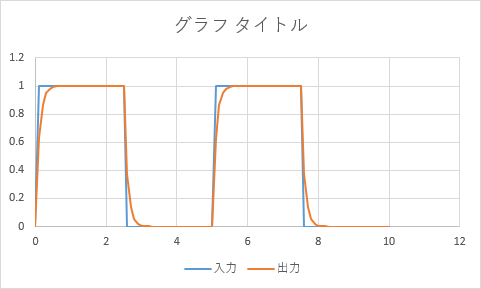
ノイズの場合はこちら。やはり変化が速くなりノイズ除去の効果が減っていることがわかる。
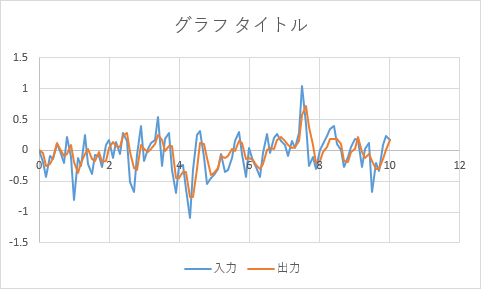
[演習問題3]
定数 RC の値を 2 に変えてシミュレーションを行え。ローパスフィルターの性質はどう変わるか。
変更箇所のは以下の通りである。
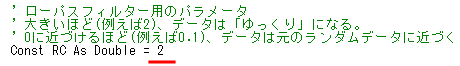
なお先程と同様、定数の値を書き換えたら、シート上で「入力:0/1の切り替え」をクリックしなおして欲しい。
0/1の切り替えの場合はこちら。時定数、すなわち時間が長くなると言うことは、遅く変化するということである。
入力の変化に追随できていないことがわかる。
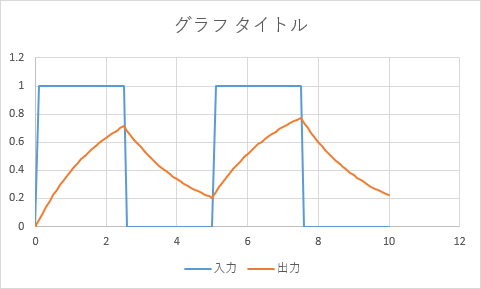
ノイズの場合はこちら。変化が遅すぎてもノイズ除去はうまくいかないことがわかる。
←1階定数係数線形微分方程式/課題→
Excel VBA で微分方程式をシミュレーションしように戻る