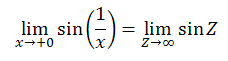Excel-05: Excel グラフの描き方・悪い例
これまで、実験データより作られるグラフを「実験グラフ」として、
理論式の分かっているグラフを「理論グラフ」として描き方をそれぞれ学んだ。
これらについて、学生がよくやりがちな「悪い例」をいくつか提示する。
このような「悪い例」に陥らないよう、綺麗なグラフの描き方をしっかりマスターして欲しい。
 金丸隆志「理系のためのExcelグラフ入門」好評発売中です
金丸隆志「理系のためのExcelグラフ入門」好評発売中です
実験に基づくデータを描く際、下図のようにデータ点を表すマーカーがないグラフを描いてしまう学生が多い。
実験グラフの場合はを必ずデータ点をマーカーで表示するようにして欲しい。
実験では点を結ぶことよりも、点そのもの(実験データそのもの)が非常に大事だからである。
実験データを滑らかな平滑線で結びたくなるという学生は多い。
しかし、平滑線の利用には問題も多く、私は平滑線の利用は避けるべきと考えている。
ここでは、その理由を記したいと思う。
まず、実験グラフの大前提から記そう。
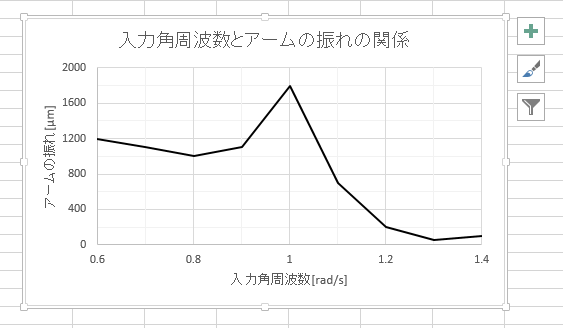
先程も述べたように、実験グラフで最も大事なのは、下図に示したように、実験で観測したデータを表す点である。
このとき、データを結ぶ線は単なる補助線にすぎないことに注意して欲しい。
言い替えれば、「実験グラフでは線よりも点が大事」ということである。
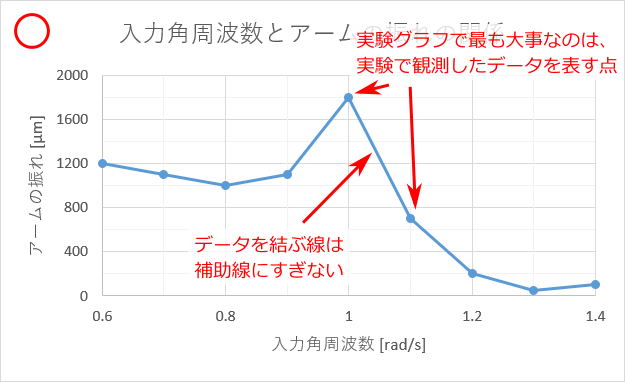
このグラフを、「散布図(平滑線とマーカー)」を用いて描くと下図のようになる。
データ点は上図と同じであるので、問題は滑らかに描かれた平滑線である。
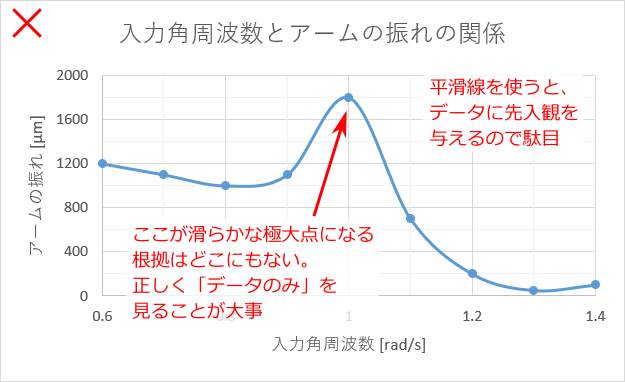
このグラフを見て「滑らかで良いじゃないか」と思った学生がいるかもしれない。
もしそう思ったとしたら、「グラフは滑らかな方が良い」という先入観をまず捨てて欲しい (少なくとも実験グラフでは) 。
なぜなら、通常の実験では、グラフが滑らかになる根拠はどこにもないからである。
すなわち、平滑線を用いたグラフは、
「グラフが滑らかになる根拠はないにも関わらず、『グラフは滑らかになるはずだ』という先入観を与えてしまう」
点が問題なのである。
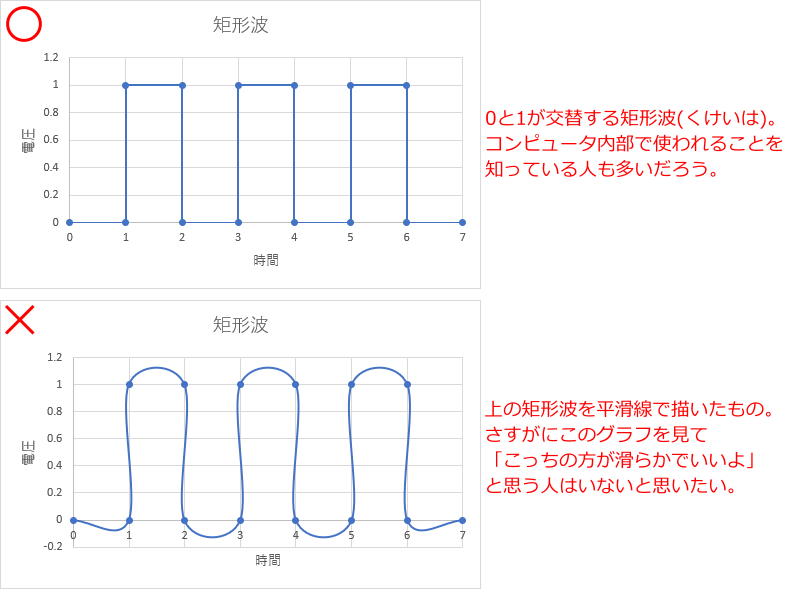
もう少し極端な例を示すと、平滑線の問題を理解しやすくなるかもしれない。
それが下図に示す矩形波の例である。
矩形波は 0 と 1 などの二つの値を交替するグラフとなるが、
これを平滑線で描くと、矩形波から大きく逸脱したグラフとなってしまう。
この図を見れば、平滑線の安易な利用に問題があることをわかってもらえると思う。
以上のように、私は平滑線の安易な利用は避けるべきと思い、そう指導しているのだが、
平滑線を利用したがる学生は後を絶たない。
本ページを見て、平滑線を利用することの問題を理解してくれる方が一人でも増えると嬉しく思う。
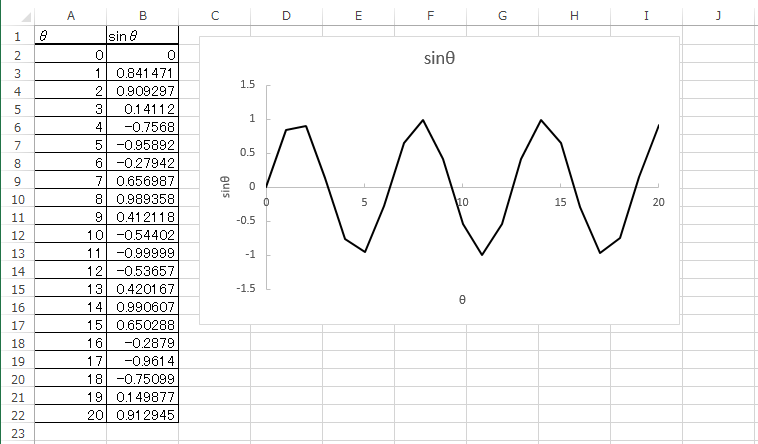
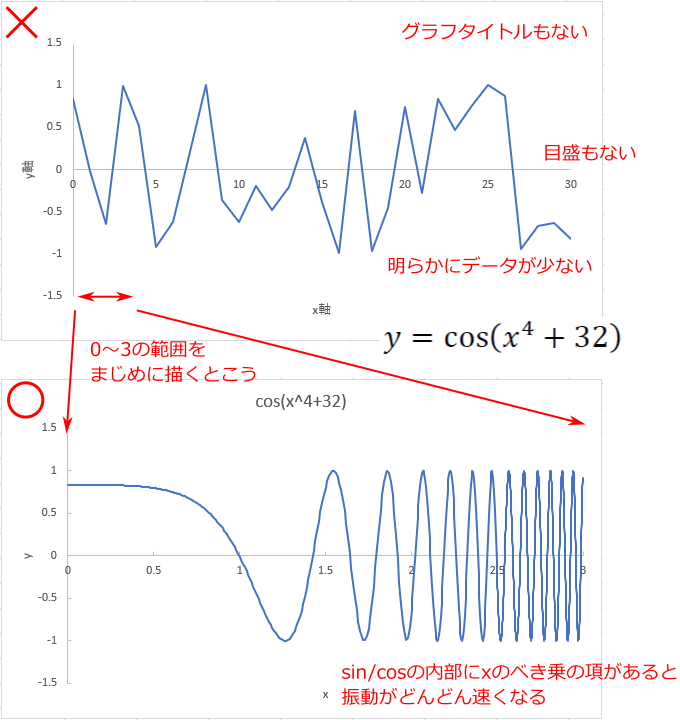
一方、理論グラフでやりがちなミスは「点が少ない」ことである。
下図のグラフを見れば、点が少なくカクカクしていることは一目瞭然であろう。
これは、点の間隔を1ずつにしていることに起因する。
実験データから作る「実験グラフ」であれば点の数に制限があるのはやむを得ないが、
理論式がわかっている「理論グラフ」ならば、十分点を多くとって綺麗なグラフを描くべきである。
特に、sin θ のグラフは (実験グラフと異なり) 滑らかになることがあらかじめ分かっているのだからなおさらである。
あらかじめどんなグラフになるか分かっていない場合の注意はページ後半にあるので読み進めて欲しい。
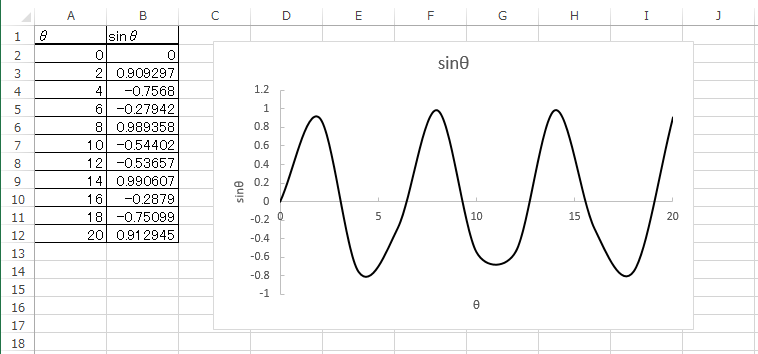
次に多いのは「点を滑らかに結んでごまかしている」グラフである。
これは上の「点が少ない」ことと関係しているのだが、
点が少ないときに点を滑らかに結ぶと、以下のように不自然なグラフになる。
なお、グラフの選択の際にで以下を選ぶと点が滑らかに結ばれるのであるが、
点が少ない時に点を滑らかに結んでもうまく行かない。
滑らかに結ぶより、点を増やすことをこころがけよう。
なお、以下の例も点が少ないのに滑らかに結んでごまかしている例である。
一見正しそうに見えるが、表をよくよく見ると sinθに対応する数が
1 と -1 の2値しか現れていない。もちろんこれは点が少なすぎるのであるが、
そこを滑らかに結んでごまかしているというわけである。
繰り返すが、
滑らかに結ぶより、点を増やすことをこころがけよう。
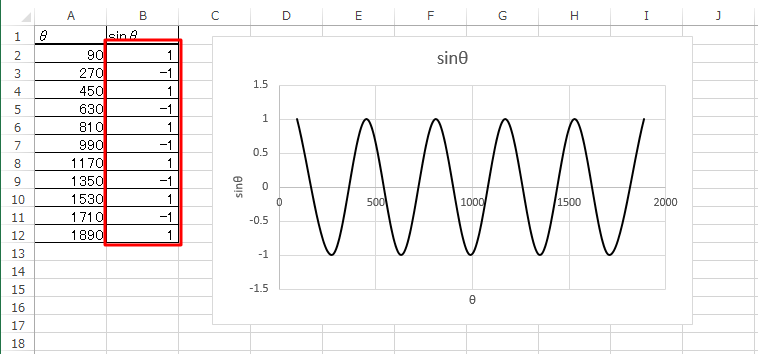
sinθのグラフの一部を描いた次の例は致命的である。
ぱっと見はどこが問題か分からないかも知れないが、
横軸 (θ軸)の値が、左側の表と全然関係ない値になってしまっている。
これは実はグラフを描くときに「散布図」ではなく「折れ線」を
選ぶと起こる現象である。
sinθに対応するθの値を、勝手に1、2、3と割り当ててプロットしている
ことになる。
もちろん、これは描きたかったグラフの横軸の値と全く異なるのであるから間違いである。
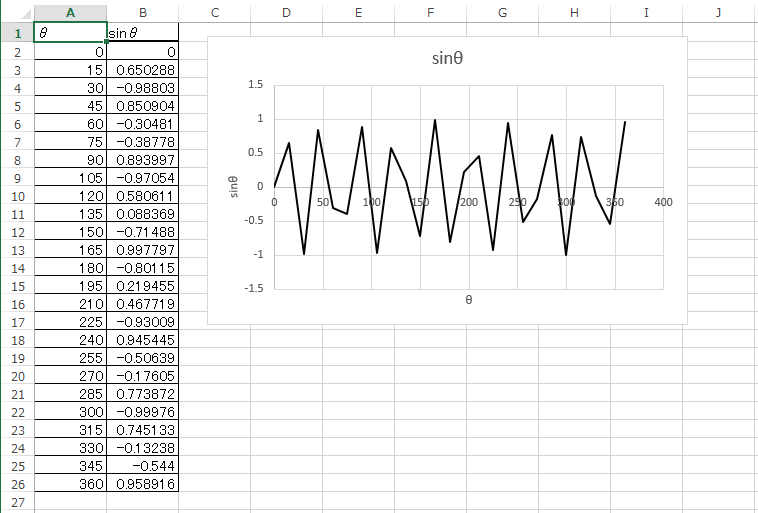
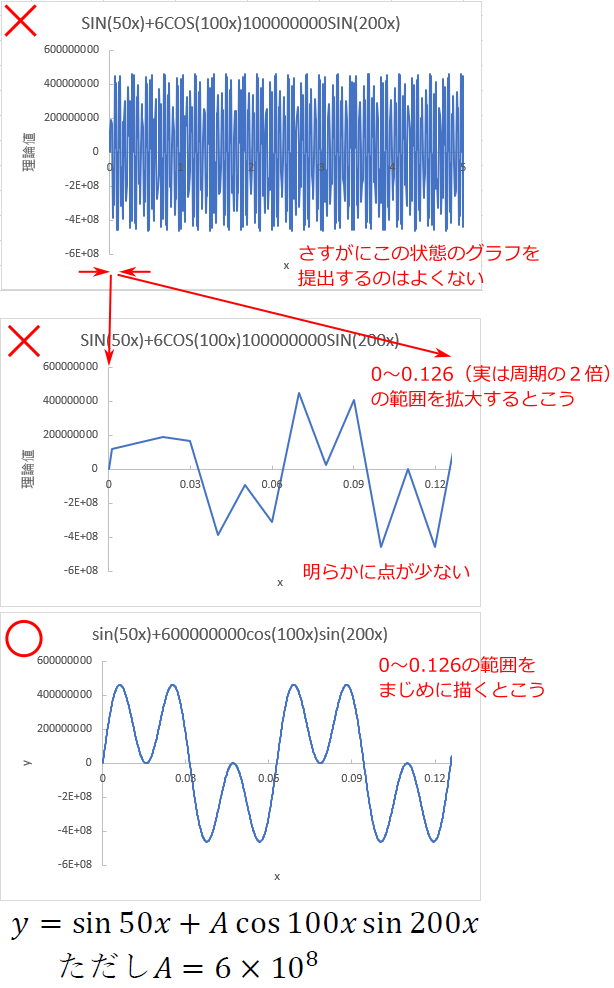
sinθの悪い例4つめは、「周期を理解していない」グラフである。
例えば、エクセルのSIN関数を用いてグラフを描くと、SIN関数はラジアン単位の値を取るので周期が2π (約6.28) のグラフになるが、
これを 0 ~ 360 の範囲で表示しているグラフが若干あった。
例えば以下の図である。本来ならばこのグラフは周期2π(約6.28) なのだが、
これを周期 360度と勝手に解釈して描いている。
このグラフが間違いであるのは、
- そもそも sinθのグラフに見えない
- θ=360 度に対する sinθの値が 0 でない
ことなどにより、言われる前に自分で気づかなければならない。
もし、周期が 360度の sin のグラフを書きたかったら、
「=SIN(A2*360/(2*PI()))」などと書くべきである。(PI()=πであることに注意)
あるいは、度の値をラジアンに変換する RADIANS関数を用いて
「=SIN(RADIANS(A2))」でもよい。
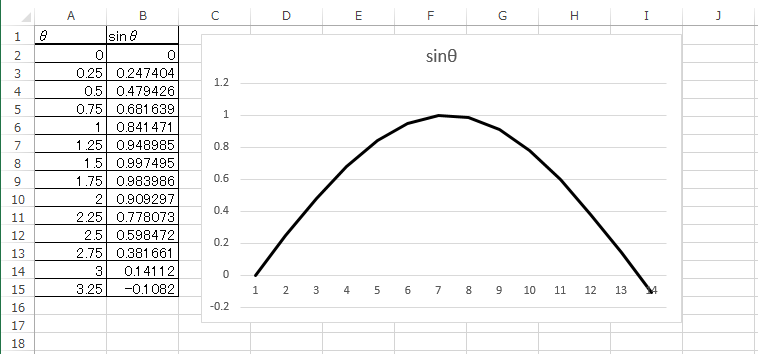
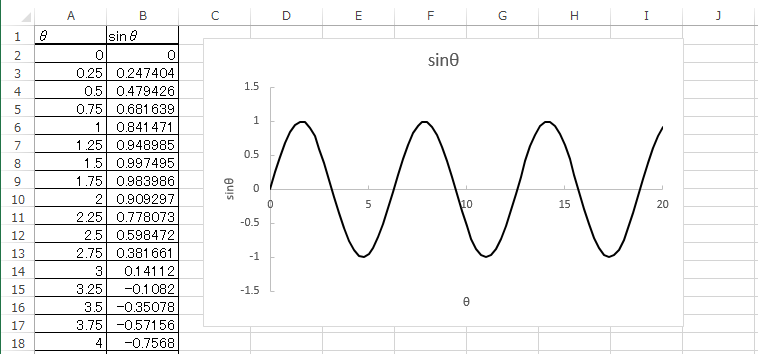
sinθの正しいグラフは以下のようである。
θを 0.25 刻みで 0~20 の範囲でデータを作成しているので、
約 80 点をプロットしていることになる。
これくらいの点(データ)を用意すれば、理論グラフとしては
十分滑らかなグラフになるのではないだろうか。
次に、tanθにおける悪い例を見てみよう。
この例は「グラフに発散があるのに無理矢理データを線で結ぶ」という点に問題がある。
tanθのグラフは (θ=±π/2、…)の位置で発散することはご存知の通りである。
そのような場合にどうすべきか、ここで身につけて欲しい。
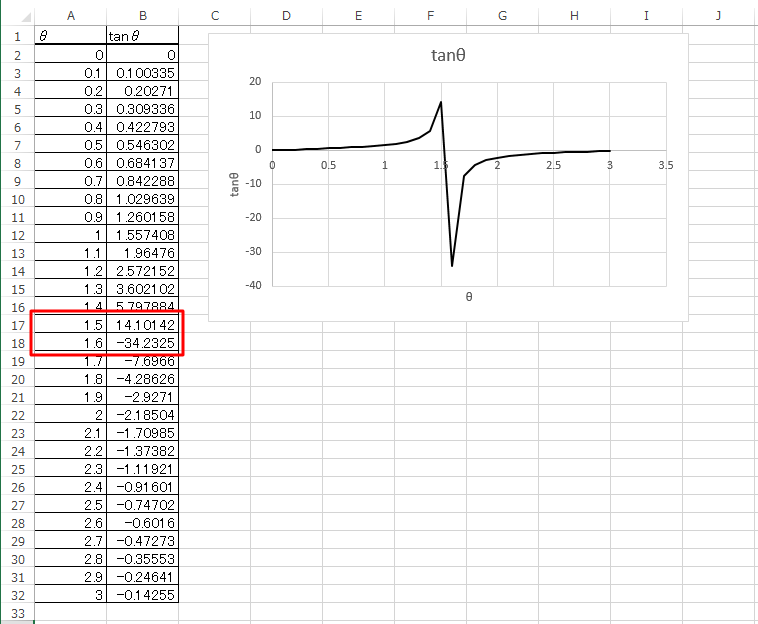
まず、悪い例は下図。tanθは θ=π/2 (約1.57) において値が発散することは知っているはずである。
そのため、下図のグラフでもその付近で値が+から-へ大きく振れている。
だが、この発散のあるグラフで+の値から-の値 (下図赤い四角) を線で結ぶのは誤りである。
では、どのようなグラフを描けば良いのか。
その例を表したのが下図である。
点を十分多くとり、さらに+から-への直線を結んでいないことがポイント。
どうすれば良いかというと、下図赤い四角のように、
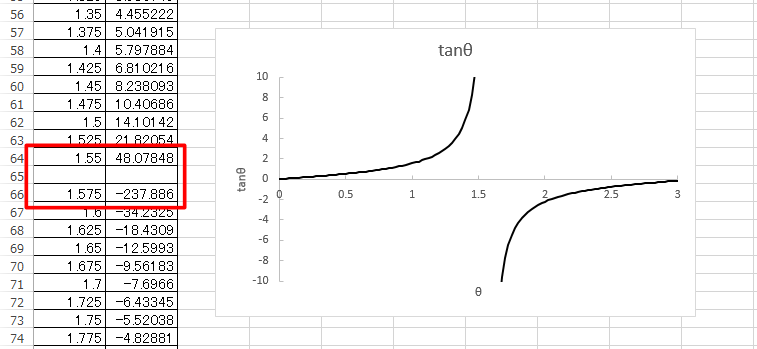
+から-へ値が変化するところに空行を一行挿入すれば良い。
空行を一行挿入するには、下図の場合、1.575に相当する行番号で
右クリックして「挿入」を選択する。
さらに、縦軸の範囲を自動から手動にし、-10~10 に固定している点も注意しておきたい。
次の例は上の tan x のグラフと同じく、グラフが発散する場合である。
やはり発散の位置を考慮しないと正しいグラフが描けない。
例えば、以下の式のグラフを描くことを考える。
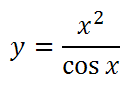
まず、何も考えずにグラフを描くとこうなる。これは発散を考慮していない点で誤りである。
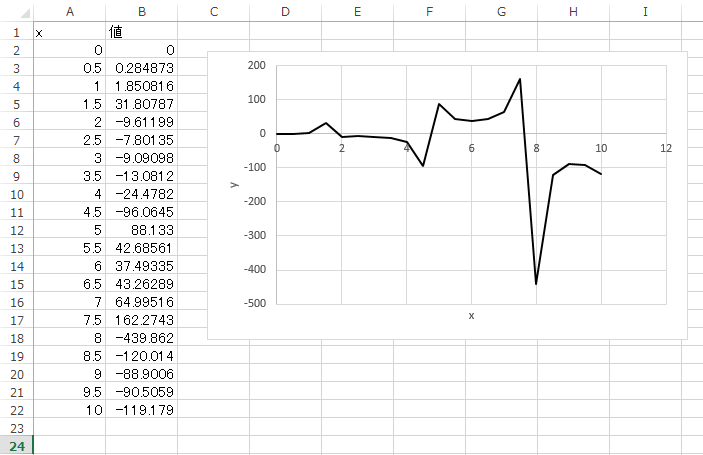
発散の位置は (分母)=0 を満たす x として求められる (0 で割ると発散するということ)。
cos(x)=0 を満たす x をラジアンで求めると、π/2、3π/2、9π/2…となる。
正しくグラフを描くと下記のようになる。
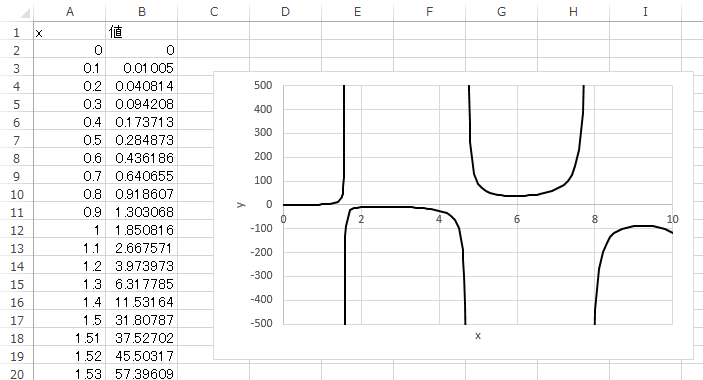
綺麗に描くために、
- 縦軸の範囲を固定
- 発散の点で一行空ける
- 発散の前後で十分細かく点を取る
などの配慮をしている。
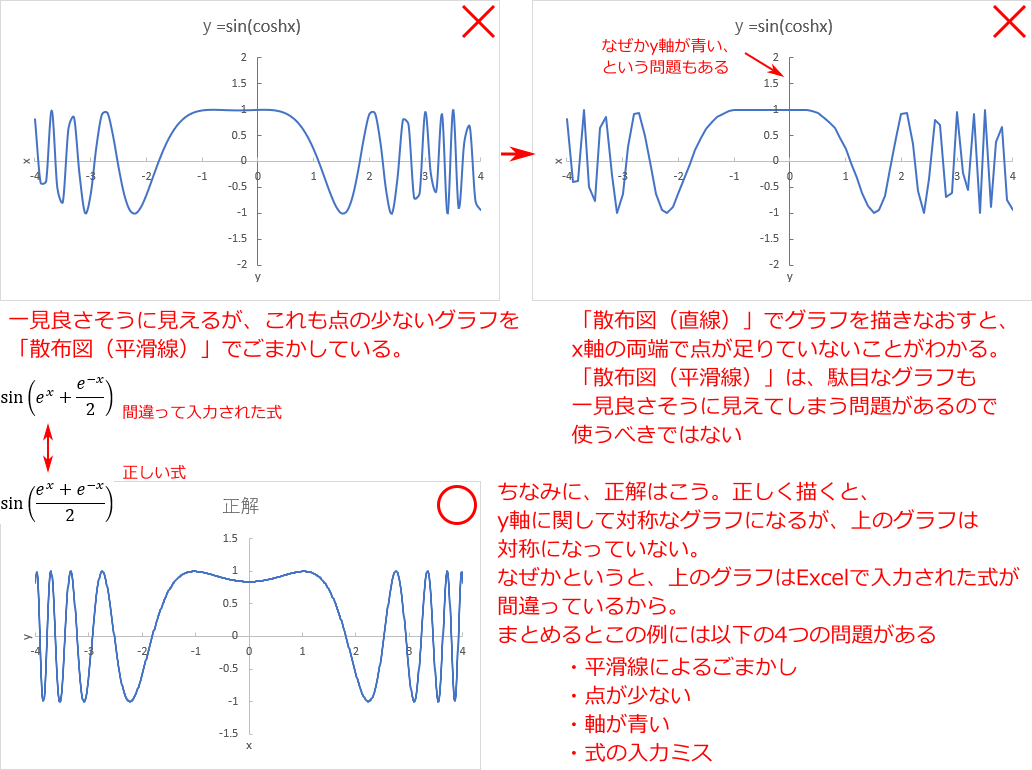
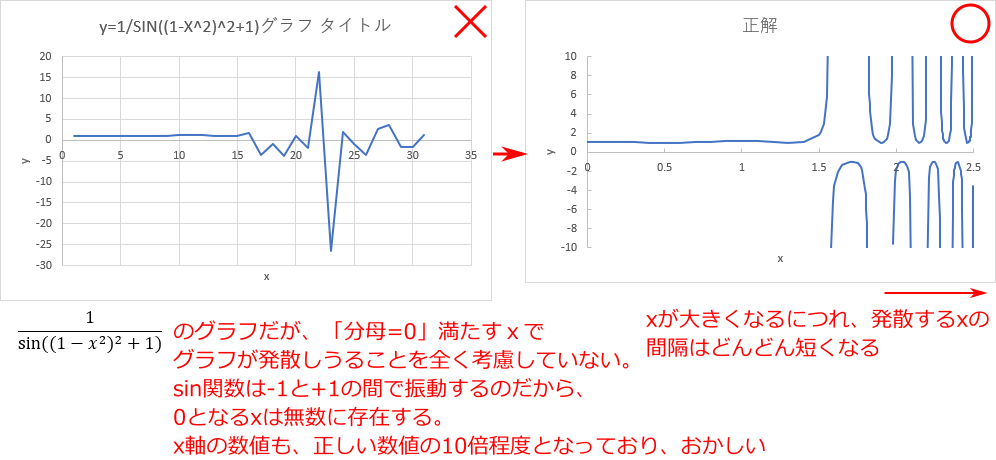
下の例は 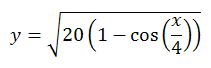 のグラフとして学生から提出されたものである。
のグラフとして学生から提出されたものである。
振り子がふれているときの、振り子の角度 x と速度 y の関係、ということで、物理に関係するグラフである。
まず気がつくのは、既に見た「点が少ないのを滑らかに結んでごまかしている」という問題である。
点の間を滑らかに結ぶよりも点を増やすことを心がけよう。
さらに、グラフをみると、山の部分はそこそこ綺麗にかけてるものの、谷の部分の変動が大きく汚くなっている。
正しいグラフはどうなるのだろうか?
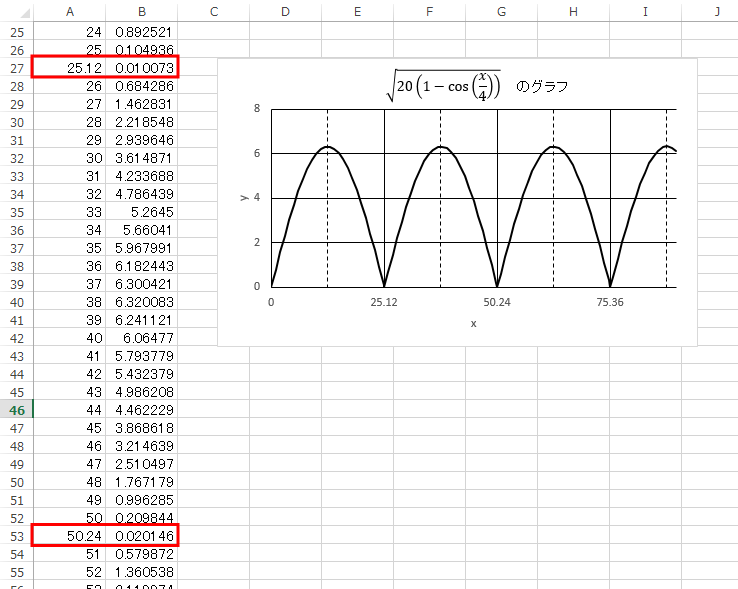
これは正解を先に提示した方が良いだろう。以下のように谷がとがったグラフになる。
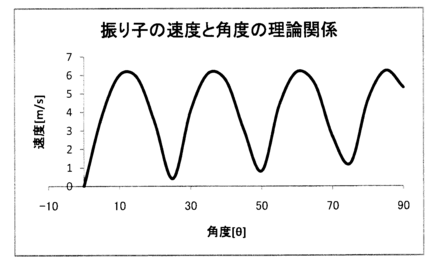
なぜこのようなグラフになるかは、以下のように高校数学の範囲で理解できる。
元の式である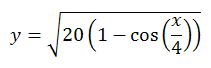 に対し、
三角関数の半角公式
に対し、
三角関数の半角公式
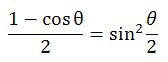
を適用すると、以下のように計算される。
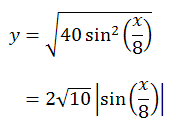
すなわち、描くべきグラフは sin の関数の絶対値 (| |) を取ったもの、ということになる。
絶対値を取るということは、絶対値の中身 (sin) のグラフを x 軸に関して、y の正の方向に折り返す、ということである。
そのため、sin のグラフが x 軸を横切る点でグラフはとがる、というわけである。
ちなみに、x 軸と接する点は x/8 = π × (整数) を満たす点であるので、
x = 8π × (整数) ~ 25.12、50.24、75.36…というわけである。
上記の正解グラフの脇の表を見ると、
- 横軸の間隔は 1 ずつであるが、25.12、50.24 のところに特別に値を設けている
ことがわかる。これは、その位置でグラフがとがることを踏まえ、なるべく値の飛びのないグラフにするためである。
このように、Excel のグラフ機能は万能ではない (コンピュータは万能ではないという言い方も出来る)。
描かれたグラフが正しいのか、おかしなところがないか、皆さん自身で数学の知識を駆使してチェックしなければならない、ということである。
次のグラフは式 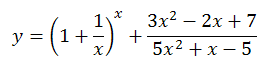 に対するグラフとして学生が提出してくれたグラフである。
に対するグラフとして学生が提出してくれたグラフである。
なかなか野心的な式であり、そもそも課題の意図としては、このように「どのようなグラフになるのか一見ではわからない」グラフを期待していた。
そういう意味で、難しい式にチャレンジしてくれたことは高く評価したい。
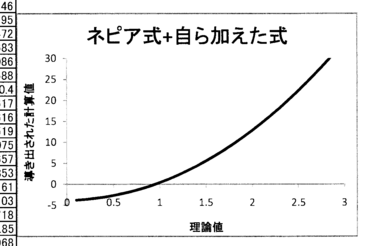
ただし、この答案は式とグラフを見たときに「あ、間違ってそう」ということが直観的にわかってしまう。
どういうことだろうか。
そのために、x の値が十分大きいときの y の値を考えてみよう。まず、式の前半の極限を取ると、自然対数の底 (ネイピア数) e になる。
(e の定義そのもの)
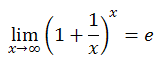
さらに、式の後半も整式の極限なので、高校数学の範囲で計算できるはず。
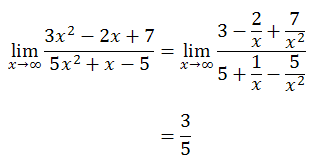
そうすると、結局、x が大きいときに y のグラフは以下の値に収束すべきだと式を見たときにわかるわけである。
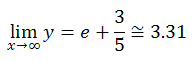
しかし、グラフはそうなっていないので、どこかに間違いがあるのだろうとわかる。
(恐らくセルに入力した式の記述が間違っていたのだろう)
正しくグラフを描くと以下のようになる。確かにおよそ 3.31 に収束していることがわかる。
なお、「整式の分母 = 5x2 + x -5 = 0」となる点、すなわち x = (-1+√101)/10 ~ 0.905 において、グラフが発散することにも注意。
(グラフは x>1 の範囲でしか描いていない)
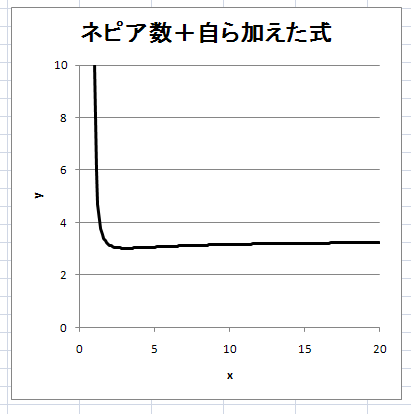
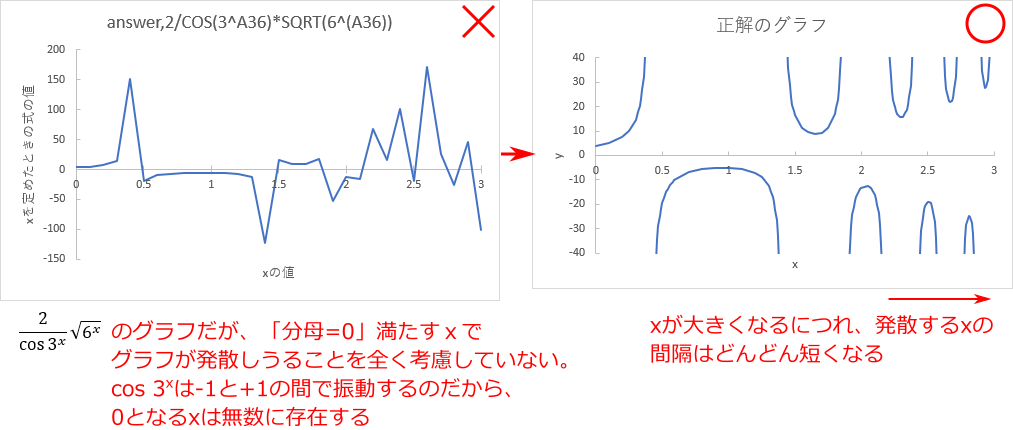
最後の例は式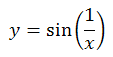 に対するグラフである。
に対するグラフである。
これもまた非常に野心的なグラフに取り組んでくれた例と言える。
提出されたグラフは以下の通り。
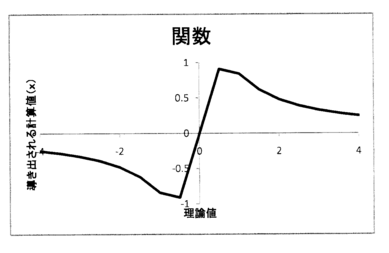
まず、このグラフには既に何度か紹介した「点が少ない」という問題がある。
しかし、「点を増やせば正しいグラフは描けるだろうか?」という問題がこの式に対しては存在する。
どういうことだろうか?
まずは点を増やしたグラフを見てみよう。なお、以下では x が正の範囲のみをグラフ化する。
(x の負の範囲は原点に対して点対称である)
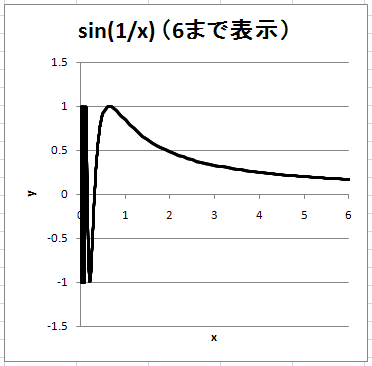
x の最大値を 6 としてグラフ化したのが下図である。x が 0 に近付くにつれ、グラフの変動が激しくなっている。
何が起こっているのだろうか?
そこで、x の表示範囲を最大 0.5 に拡大してみよう。すると下図のようになる。
やはり x が 0 に近付くにつれ、変動が激しくなる。
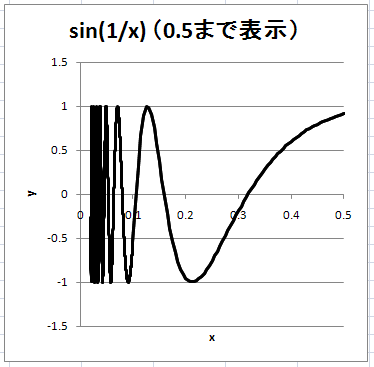
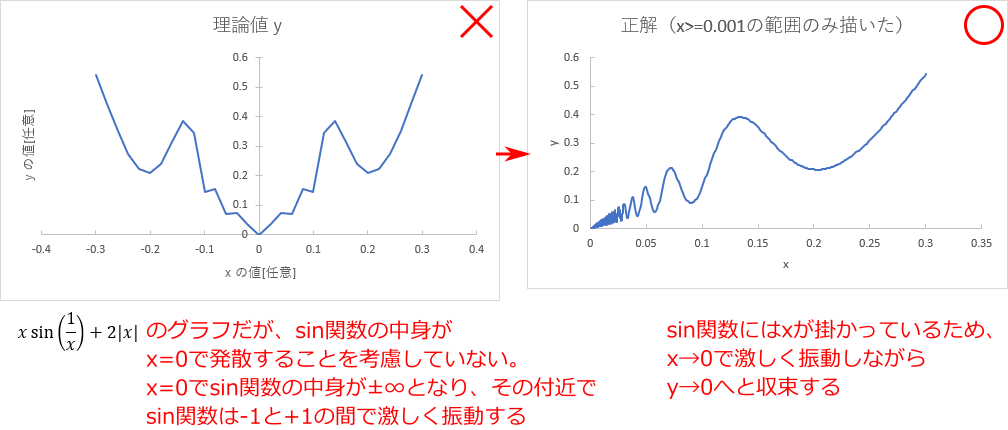
最後に、0.02<x<0.1 の範囲の表示。振動はどんどん速くなっていることがわかる。
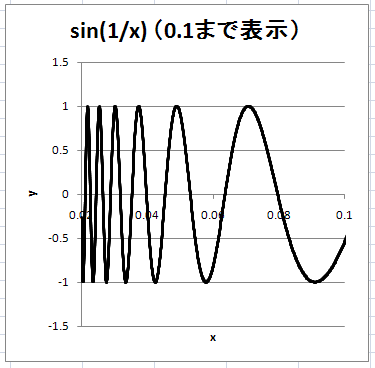
つまり、 x が 0 に近付くほど、y はどんどん速く振動する、というわけである。
この理由もよく考えると理解できる。
まず、x が正の側から 0 に近付いたときは以下のように sin の中身が無限大になる。
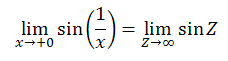
sin の中身が無限大になるとき (x が 0 になるとき)、sin の値は常に -1 と 1 の間を変動し続けるので、
いつまでたってもどこかの値に収束するということはない。
すなわち、x = 0 におけるグラフの値は存在しない。
そのため、上のグラフも、x> 0.02 の範囲でしか描いていない。
それ以下の範囲では振動の速さが無限に速くなり、無限に細かな点が必要になるからである。
以上、グラフ描画においていくつかの悪い例を見てきた。
- 点が少ないのでグラフの正しい形状を表示していない (「本来通るべき点を通っていない」「とがっている」など)
- 発散を正しく処理していない
- 入力式にミスがあるためグラフが間違っている
- 本当は描けないグラフを描いてしまっている
などの問題があったが、これらの問題に対して Excel が「間違っているよ」と指摘してくれるわけではない。
Excel は (あるいはコンピュータは) 皆さんが指示した通りの計算と描画を忠実に行うだけである。
結局、グラフが適切かどうかは利用者である皆さんが判断するしかない。
そういう意味で、いくらコンピュータが発達しようと、数学 (や物理) の知識が不要になることはない、ということは注意しておいて良いだろう。
研究の分野では、ときどき「研究で Excel を使うべきではない」という意見が出ることがある。
研究には様々な分野があり、その分野で使われる標準のツール群がある。
Excel がその標準ツール群に含まれていない、ということは実際あり得るだろう。
とは言え、Excel というのは単なる道具であるから、その道具を正しく使う限りにおいて役に立つ場面は多いだろう、と私は考えている。
しかし、学生を指導する場面で「Excel を正しく使うのは難しいことなんだなあ」と実感することは多い。
このページで取り扱ったグラフ描画の指導をするときは特にそうである。
以下に挙げる、学生が自由に式を決めて描いたグラフの添削例を見ると、Excel を正しく使うことの難しさを実感できるかもしれない。
(教科書などから式を拾ったのかもしれない)
←Excel-04: Excel を用いたグラフの作成 (理論グラフ設定)/
Excel-06: Excel での印刷の設定→
Microsoft Office の基礎に戻る
 金丸隆志「理系のためのExcelグラフ入門」好評発売中です
金丸隆志「理系のためのExcelグラフ入門」好評発売中です













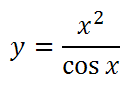


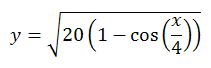 のグラフとして学生から提出されたものである。
のグラフとして学生から提出されたものである。

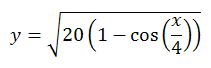 に対し、
三角関数の半角公式
に対し、
三角関数の半角公式
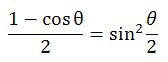
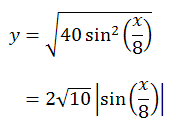
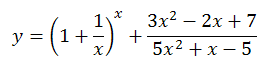 に対するグラフとして学生が提出してくれたグラフである。
に対するグラフとして学生が提出してくれたグラフである。
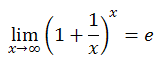
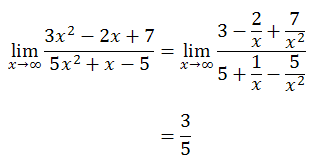
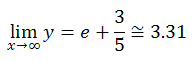

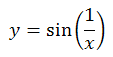 に対するグラフである。
に対するグラフである。