

: 符号付き数の除算
: 乗算と除算
: [問題] 符号付き数の乗算
やはり、正の数のみによる除算を考える。
この場合も筆算による計算が有効である。
図 10:
筆算による除算の実行。
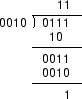 |
図 10 は 0111 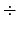 0010 (7
0010 (7 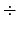 2) を計算を
筆算で行い、商 11 と 剰余 1 を得ている。
2) を計算を
筆算で行い、商 11 と 剰余 1 を得ている。
このアルゴリズムをハードウェア実装するために
流れ図で書くと、図 11 のようになる
(教科書や授業の「第一のアルゴリズム」である)。
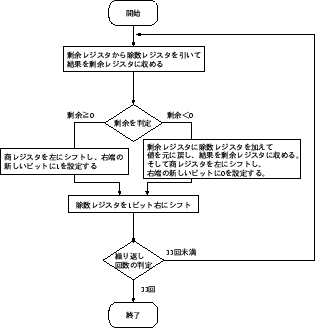
図 11:
第一の除算アルゴリズムの実行の流れ図
 |
さらに、このアルゴリズムを 0111 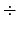 0010 に適用すると
図 12 のようになる。
0010 に適用すると
図 12 のようになる。
図 12:
第一の除算アルゴリズムを 4 ビットの除算に適用した様子。
![\begin{figure}\begin{tabular}{c\vert l\vert c\vert c\vert c}
サイクル & ステップ...
...x{3.2ex}[0pt]{5} & (c) & 0011 & 0000 0001 & 0000 0001
\end{tabular}
\end{figure}](img41.png) |
初期状態において、除数は 8 ビットの内上位 4 ビットにセットされ、
被除数は剰余の下位 4 ビットに収められていることに注意しよう。
[問題]
- 図 12 における (a)、(b)、(c) は図 11
の流れ図の何に対応しているか。
平成16年12月13日
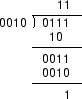
![]() 0010 (7
0010 (7 ![]() 2) を計算を
筆算で行い、商 11 と 剰余 1 を得ている。
2) を計算を
筆算で行い、商 11 と 剰余 1 を得ている。
![]() 0010 に適用すると
図 12 のようになる。
0010 に適用すると
図 12 のようになる。