[問題] 2 の補数表現

本章ではコンピュータ内での数値の表現を復習する。 本章の内容の多くは論理回路の授業や演習で扱った内容の復習であるはずなので、 付録として収録する。

コンピュータ内では数値は 2 進数で表現される。 数値は多くの場合正負の数の両方を取り扱うが、例えばメモリアドレス のように常に正の数しかあつかわない場合がある。 前者は「符号付き数」として表現され、 後者は「符号なし数」として表現される。

符号なし数は常に正の数であるので取り扱いは簡単である。 たとえば 4 ビットの 2 進数 $1010$ は、 $2^{3} + 2^{1}$ であるから 10 進数の 10 を表している。

符号付き数、すなわち正負の数の 2 進数での表現は、 コンピュータの黎明期には様々な手法が試みられたが、 現在は「2 の補数表現」が用いられる。 2 の補数表現された 4 ビットの 2 進数と 10 進数の対応は以下のようになっている。

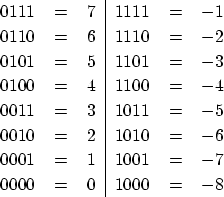
正の数は符号なしの場合と同じである。 ただし、最上位ビット (most significant bit: MSB) は つねに 0 でなければならないので、表せる最大の数は 7 である。 一方、負の数の場合は 最上位ビットは 1 であることに注意しよう。

一般に $n$ ビットの場合、 $-2^{n-1} \sim 2^{n-1} -1$ の範囲の数値を 表現できる。(0 があるので、正の数のほうが 1 つだけ少ない)

負の数をこのように 表現する理由は、ハードウェア (加算器) の構成が簡単になるからである。 例えば 「負の数を含んだ加算を統一的なアルゴリズムで実現できる」、 また「正負の反転が (次章でみるように) 簡単にできるため、減算器 も加算器を利用して簡単に構成できる」などのメリットがある。

[問題]

1. 4 ビットの 2 進数 1010 がある。これが符号なし数であるとすると、10 進数でいくつになるか。
2. 4 ビットの 2 進数 1010 がある。これが符号付き数であるとすると、10 進数でいくつになるか。