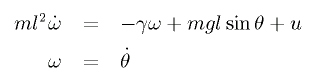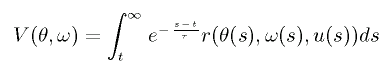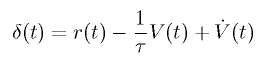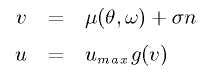強化学習による振り子の振り上げ制御



tp_rl_app.jarをダウンロードしてダブルクリックして実行してください(コマンドラインでは java -jar tp_rl_app.jar)。

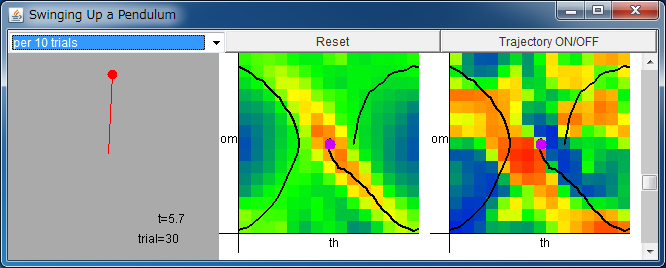
左から順に、振り子の状態、Critic、Actor。

Critic/Actor の横軸は -π <θ < π、 縦軸は -2π <ω < 2π を表す。
値は、青：負、緑：0、赤：正を表す。

Critic/Actor のフィールドをクリックすると、初期状態を定められます。
スクロールバーによりおもりの質量を変更できます。

trial が 50～100 程度まで学習すると振り上げが可能になります。

シミュレータが実行出来ない方は adoptium.net からOpenJDKをインストールしてください。

強化学習を用いて振り子を鉛直上向きに静止させる制御を考えます。
トルク u の加わった振り子の運動方程式は次式になります。



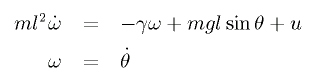
このとき、振り子の状態 (θ, ω) を観測し、その状態に応じた トルク u を出力する制御器を構築するのが課題となります。

強化学習では、下図のような構成で制御を行います。



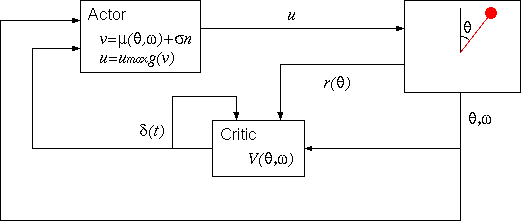
まず、系の状態に応じた報酬 r は 振り子の振り上げ時が最大となるよう r(θ) = cos θ で定義されます。
このとき、方策 u に従った時に期待される報酬 V(θ, ω) は次式で定義されます。



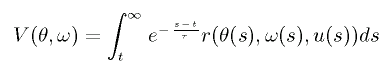
V(θ, ω) が大きくなるように制御を行うと、系は所望の状態に近付くことになります。

しかし V(θ, ω) は未知の関数なので、実際には関数近似を行って V(θ, ω) を推定することになります。
このとき、以下の TD 誤差が小さくなるようにパラメータの変更を行うと、 V(θ, ω) が推定されます。
このように、V(θ, ω) を推定するユニットを Critic と呼びます。



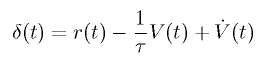
一方、(θ, ω) の値に応じて制御入力 u を決めるユニットを Actor と言い、以下の式に従います。 (n はノイズ)



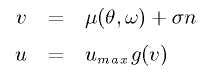
μ(θ, ω) も未知関数であり、関数近似を行う必要があります。
μ(θ, ω) の推定においても、上記の TD 誤差を小さくする ようにパラメータを変更することで、学習が進みます。

ここでは、Critic の学習に連続時間、連続空間の TD(λ) 法、 Actor の学習に方策こう配法を用いています。

このページは以下の文献を参考にしています。

←「強化学習による Cart-Pole Balancing」へ

金丸隆志のページに戻る