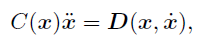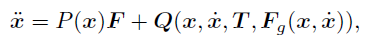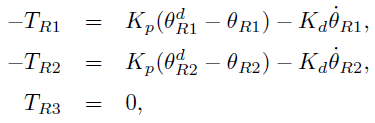二足歩行モデルの手動制御
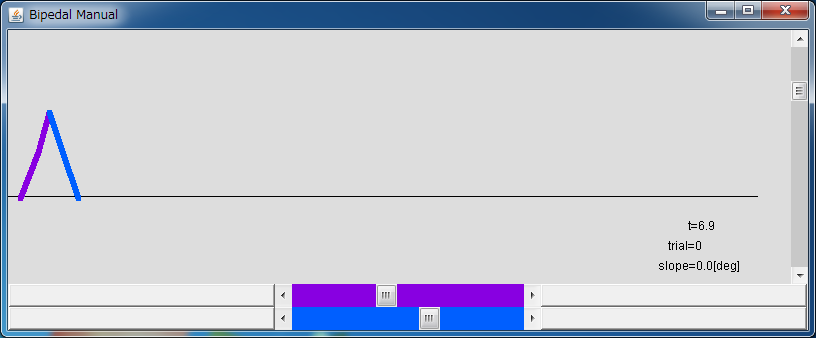
bw_manual_app.jarをダウンロードしてダブルクリックして実行してください(コマンドラインでは java -jar bw_manual_app.jar)。
強化学習による二足歩行モデルの制御との比較のために、
同じ二足歩行モデルを手動で制御してみましょう。
二足歩行の制御が案外難しいものであることが体感できるはずです。
シミュレータが実行出来ない方は adoptium.net からOpenJDKをインストールしてください。
[操作方法]
- 青か紫の水平バーをダブルクリックすると、モデルに水平方向の初速度が与えられます (一度のみ)。
- 青（右足）か紫（左足）の水平バーを動かすことで、モデルの足の目標角が変化します。
片方の足を動かすだけで、もう一方の足の目標角は自動的に決定されます。
ここで用いている二足歩行モデルは Taga (1991) らが用いたもので、8個の制約条件
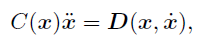の元での14変数についての運動方程式
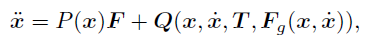で書き表せます。
14 - 8 = 6 ですから、このモデルの位置は
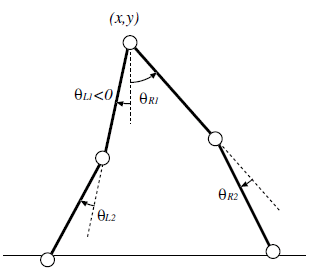
腰の位置 (x, y) および
両足の腰と膝の角度
(θR1, θR2,
θL1, θL2)
の計6変数で表せます。
さらにこれらの時間微分
(vx, vy) および
(ωR1, ωR2,
ωL1, ωL2)
も考慮することで力学系としての系の状態が指定されます。
ここで、この二足歩行モデルに与えるトルク T は
PD 制御則により決定されるとしています。
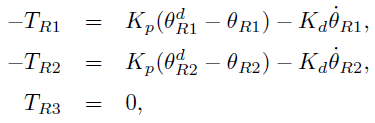このアプレットでは、右足と左足の目標角
θR1d と
θL1d とを指定しています。
θR2d と
θL2d は、
θR1d > 0 かつ ωR1d > 0 のときにθR2d=55 でそれ以外では
θR2d=0 のように自動的に定めています。
このページは以下の文献を参考にしています。
- [二足歩行モデルについて]
G. Taga, Y. Yamaguchi, and H. Shimizu,
"Self-organized control of bipedal locomotion by neural oscillators in unpredictable environment"
Biological Cybernetics, vol. 65, pp.147-159 (1991).
←「強化学習による CPG 入力下二足歩行モデルの制御」へ
／
「強化学習による Cart-Pole Balancing」へ→
金丸隆志のページに戻る