エノン写像のアトラクターギャラリー

|
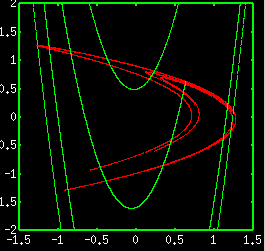
エノン写像のアトラクターは、次の離散時間写像により生成されます。
xn+1=1-axn2+byn yn+1=xn ここでは a=1.4, b=0.3 の場合について実験を行いました。 フラクタル性をもつ「アトラクター」(赤い曲線) が見られます。 緑の曲線は、アトラクター上の不動点から発する安定多様体と呼ばれる不変集合です。 アトラクターと安定多様体は無限に交差し、細かい網を形成します。 また、アトラクターと安定多様体には接点も存在するため、 エノン写像は非双曲力学系に分類されます。 非双曲力学系は接点の存在しない双曲力学系に 比べて数学的な取り扱いが難しいため、 エノン写像のようにシンプルな系でも分かっていないことがたくさんあります。 また、「エノン写像のアトラクター」シミュレータではアトラクターを拡大したり、 リアプノフ数を計算することができます。 |