Lorenz Attractor
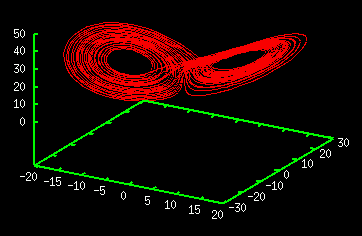

Lorenz attractor is generated by three-dimensional differential equation written as
Because this equation has nonlinear terms, that is, xy and xz, there is no analytic solution and we must rely on numerical simulation to derive the solution. A path from an initial point is derived using Runge-Kutta method, and drawn in three dimensional space. Almost all paths fall on the same set. The set is called attractor. |
|
Like Lorenz attractor and Rössler attractor, chaotic attractors typically have the "bunch of string" structure. This is called "self-similarity" or "fractal".
You can observe Lorenz attractor from various view angles with "Lorenz attractor" simulator. You can observe Lorenz attractor from a rotating viewpoint around the attractor with "Lorenz attractor" animation. |