Attractor of Hénon Map
|
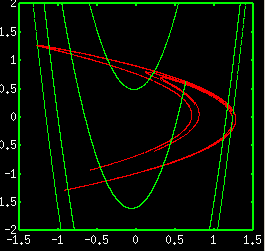
An attractor of Hénon map is generated by the discrete-time map written as
xn+1=1-axn2+byn yn+1=xn. The above figure is obtained for a=1.4 and b=0.3. We can see an attractor with fractal structure (shown by red curve). You can also see the stable manifold of the fixed point on the attractor (shown by green curve). The attractor and the stable manifold intersect infinitely, and form the infinitely fine net. There also exist points of tangency between the attractor and the stable manifold, thus the Hénon map is classified as the non-hyperbolic dynamical system. The mathematical treatment of the non-hyperbolic dynamical system is difficult, thus there are many unsolved problems even for the Hénon map. In the page of "Attractor of Hénon map" simulator, you can expand the Hénon attractor and obtain the lyapunov number. |
<< Rössler Attractor / Attractors of Periodically Forced Pendulum >>
Introduction to Chaos and Nonlinear Dynamics