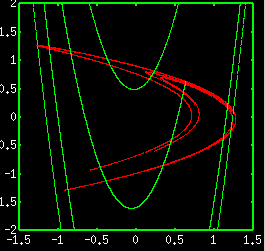
以下でリアプノフ数の計算方法を示しましょう。やや専門的になりますので飛ばして頂いても構いません。
まず、Xt+1 = F (Xt) で表されるエノン写像系の
点 Xt+1= (xt, yt) における軌道拡大率を

で定義します。DF(Xt) は点 Xtにおけるヤコビアン行列、
u1(Xt) は点 Xtにおけるアトラクターに対する単位接ベクトルです。
この軌道拡大率を用いて、粗視的軌道拡大率を

で定義します。これは n 個の点の軌道拡大率を平均したものです。
アトラクターの色はこの粗視的軌道拡大率に基づいて決められていますが、
これは後で解説します。
粗視的軌道拡大率を n →∞ の極限をとることで、最大リアプノフ数が

と計算されます。リアプノフ数はほとんど全ての初期点 X0に対して一定値を取ります。
このシミュレータでは 10000 ~ 500000 回の平均を取ることでリアプノフ数を求めています。
アトラクタのサイズを変更したり「Resize or Redraw」ボタンを押すとリアプノフ数が再計算されますが、
試行ごとに値が微妙に変化します。これは平均回数が有限であることの影響です。
さて、リアプノフ数は初期点 X0 にほとんど依存しませんが、粗視的軌道拡大率は
n が有限であるため、初期点 X0 に依存します。
シミュレータ上のアトラクターはこの粗視的軌道拡大率に基づいて色づけられています。
黄色は粗視的軌道拡大率が小さいことを、赤色は大きいことを意味します。
デフォルトでは n=1 ですので、これは軌道拡大率そのものです。
アトラクターのカーブの部分では軌道拡大率が負の値を取りますから、
黄色になっているのがわかるでしょう。
なお、アトラクターの尖った部分も拡大すると滑らかな曲線になっており、
黄色になっています。
n を 1 から大きくして行くと粗視的軌道拡大率は軌道の情報を取り込みながら
アトラクター上で様々な値をとります。
例えば、 n=5 にセットし「Resize or Redraw」ボタンを押してみましょう。
アトラクター上に黄色の領域がまばらに現れるでしょう。
これらの点は、以後の 5 ステップ以内に曲線のカーブの領域を通過する点です。
より専門的に言うと黄色い領域は、「エノン写像のアトラクター」ギャラリーで紹介した安定多様体とアトラクターの接点の軌道を反映しています。
このように、粗視的軌道拡大率の統計性はアトラクターの空間構造を反映しています。
なお、n を大きくすると粗視的軌道拡大率はリアプノフ数に近付くため、
アトラクターの色は一様になってゆきます。
このページは以下の文献を参考にしています。
|