第七回 学生用演習(2)
学生用演習問題の第二回である。今回は少しだけ課題に「考える」要素が加わる。本講義の過去の資料を探せばヒントは見つかるが、皆さんがそれに気づくかどうかはわからない。
今回の課題はこちら。
見やすいよう画像形式でも問題を提示する。
さて、この問題は時間 t の関数 θ(t) の一階微分方程式であるので、第四回で用いた1階定数係数線形微分方程式を数値的に解く Excel マクロ
1d-LinearDifEq.xlsmを用いる。
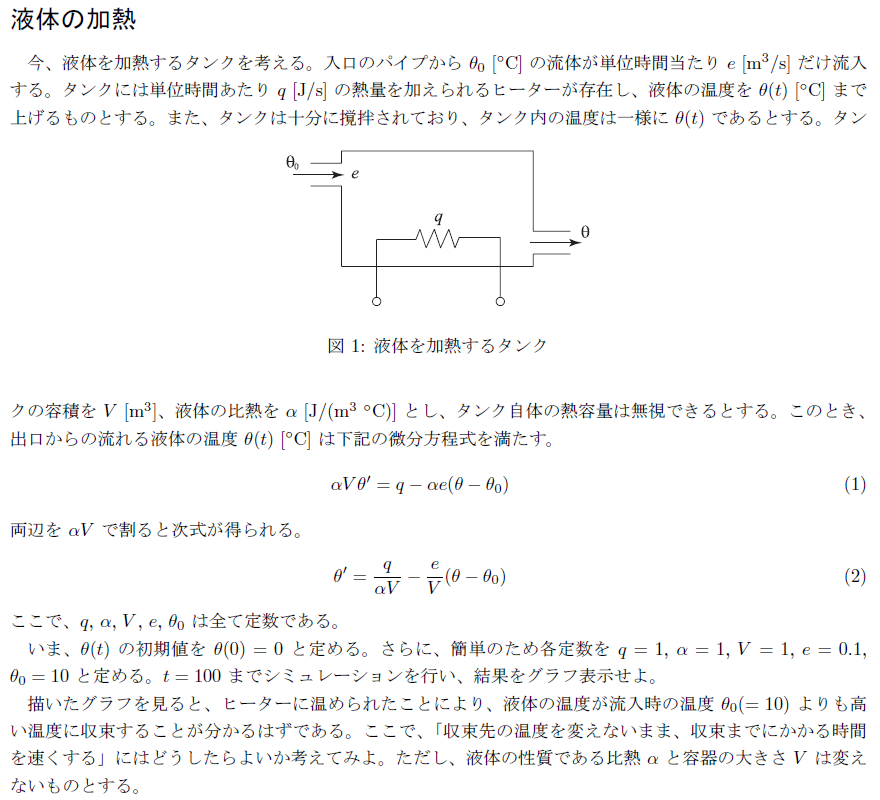
問題文中で「θ(t)の初期値を θ(0)=0」とあるが、これはプログラム中に以下の部分を編集すれば良い。
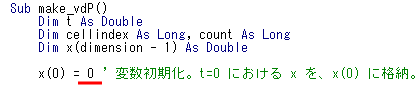
問題文中で「簡単のため各定数を q=1, α=1, V=1, e=0.1, θ0=10」とあるが、これはプログラム中で以下のように定数を追加すれば良い。
α の定数名を alpha、θ0 の定数名を theta0 としていることに注意すること。
さらに、定数 e の値は (1 ではなく) 0.1 であること、定数 theta0 の値は 10 であることにも注意。
問題文中で「t=100までシミュレーション」とあるが、これはプログラム中で以下の部分に対応し、
10 から 100 に変更しなければならない。

なお、そのままでは Excel のシート上のデータ数が大きくなりすぎるので、
以下のように、writeRate という定数の値を 10 から 50 に変更すること。
これは、シートにデータを書き込む回数を「10 回に 1 回」から「50 回に 1 回」に変更し、
データ数を減らす役割がある。

最後に、微分方程式は以下のように記述する。かっこの使い方にも注意すること。

シミュレーションを実行し、今まで通りグラフを描画してみよう。
温度はある値まで上昇することが分かるはずである。
あとは「収束先の温度を変えないまま、収束までにかかる時間を速くする」グラフを作製するにはどうしたら良いか、考えてみよう。
課題→
Excel VBA で微分方程式をシミュレーションしように戻る





