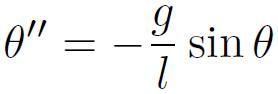第三回-02 線形と非線形をシミュレーションで確認
下図のような振り子の運動を考えよう。おもりとばねによる単振動と同じく皆さんにお馴染みの例である。
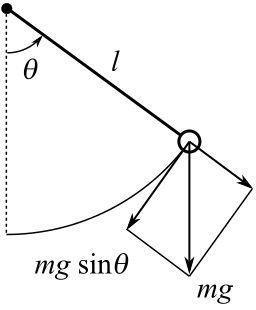
回転の運動方程式は次式のように書ける。
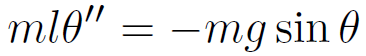
両辺を ml で割れば、次式のようになる。これは、時刻 t の関数 θ(t) についての微分方程式である。
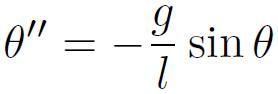
さて、前ページの内容に従えば、この微分方程式には sin θ という項が含まれるので、線形微分方程式ではない。
すなわち、非線形微分方程式である。
通常、非線形微分方程式は解析解 (厳密解、理論解) を得ることが出来ないことが多い。
ただし、実はこの振り子の運動方程式に対しては解析解が得られることが知られている。
「振り子 楕円関数 解法」で検索すると見つかるだろう。
しかし、その解法はかなり複雑であるため講義では取り扱われないことが多いし、実際皆さんも学んだことがないはずである。
では、皆さんが振り子の運動について学んだときはどうしたかというと、
θ が十分小さいと仮定し、

という近似 (線形近似という) を導入して運動方程式を以下のように書き換えたはずである。
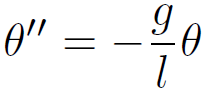
これは、ばねとおもりの単振動系の運動方程式 x'' = - (k/m) x と本質的に同じであるので、
振り子の振動を単振動として理解できたのだった。
なお、なぜ θ が小さいときに線形近似

が成り立つかは、下図のように y = sin θ のグラフと y = θ のグラフを描けば一目瞭然である。
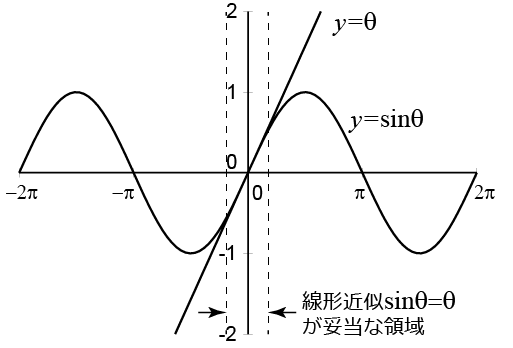
原点付近で y = sin θ のグラフと y = θ のグラフはほぼ重なっているから線形近似が成り立つのである。
注意しなければならないのは、線形近似が成り立つのは θ が小さい (振り子の振れ幅が小さい) ときのみだということである。
その範囲を超えると、振り子は単振動とは異なる運動をすることになるだろう。
それをシミュレーションで確かめてみよう。
まず、線形近似した振り子のシミュレーションからはじめよう。
そのためのマクロ PendulumLinear.xlsmをダウンロードして開いて欲しい。
「開発」タブ→「Visual Basic」ボタンでプログラムを開くと以下のプログラムが開く。
「開発」タブがないという学生は、第一回のページをもう一度学びなおすこと。
今回着目して欲しい箇所が赤で示されている。まず、運動方程式が線形化されたものが記述されていることを確認して欲しい。

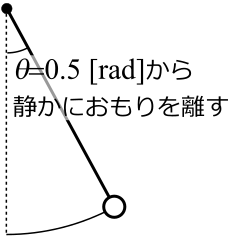
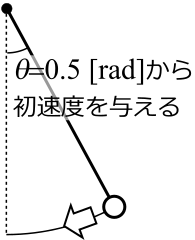
また、初期位置が 0.5 [rad]、初速度が 0 [rad/s] であることを読みとって欲しい。rad は角度の単位ラジアンである。
これは、下図のように θ=0.5 [rad] の位置から静かにおもりを離して運動を開始することを意味する。
「データ作成」ボタンをクリックし、A 列と B 列を散布図(直線) で表示しよう。
その方法が分からない学生は、第一回のページをもう一度学びなおすこと。
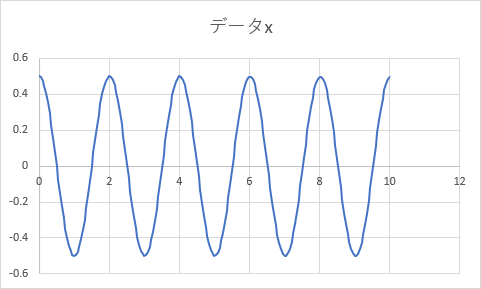
以下のグラフが現れるはずである。これは振り子の単振動を表している。±0.5 [rad] (およそ 28.6 度) の幅で振り子が振れていることが読みとれる。
ここで、下図のようにプログラム中の初速度を 0 から -6 に変更しよう。

これは、初速度 -6 [rad/s] を与えて運動を開始することを意味する。
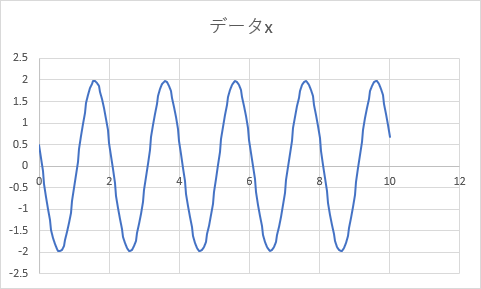
「データ作成」ボタンをクリックすることでグラフが更新される。
ほとんど変化がないように見えるが、縦軸の角度の範囲が変化している。±2 [rad]はおよそ±114.6 度である。
ちなみに、±2 [rad] という範囲は、 が成り立つ範囲を大きく逸脱している。
が成り立つ範囲を大きく逸脱している。
そのため、上図はもともとの振り子の現象とはかけ離れたグラフとなっているはずである。
それを次に確かめてみよう。
ここで、ファイル PendulumLinear.xlsm を閉じよう。ファイルの変更内容は保存してもしなくてもよい。
このファイルを閉じないと、次のシミュレーション実行時にどちらのプログラムを編集しているのか混乱してトラブルのもとである。
次ぎに、線形近似していない振り子のシミュレーションを行おう。
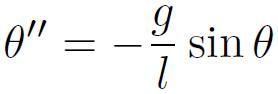
そのためのマクロ Pendulum.xlsmをダウンロードして開いて欲しい。
「開発」タブ→「Visual Basic」ボタンでプログラムを開くと以下のプログラムが開く。
先程と同様、着目して欲しい箇所が赤で示されている。まず、運動方程式が線形化されていない (sin の項がある) ことを確認して欲しい。

デフォルトの初期位置は先程と同じく 0.5 [rad]、初速度が 0 [rad/s] である。
「データ作成」ボタンをクリックし、A 列と B 列を散布図(直線) で表示しよう。
振れ幅が ±0.5 [rad] と小さいので、線形近似した場合とかなり近いグラフが得られる。
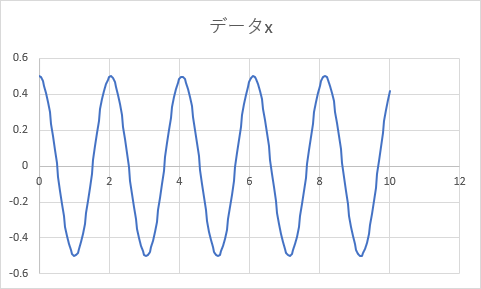
ここで、下図のようにプログラム中の初速度を 0 から -6 に変更して再び「データ作成」ボタンをクリックしよう。

以下のようなグラフが現れる。まず、線形化された運動方程式とは大きくことなるグラフであることに注意して欲しい。
振れ幅は ±3 [rad] (およそ±171.9 度) で、鉛直上方向に振り子が向く直前まで行っていることがわかる。
それにともない、振動の周期も長くなっている (ゆっくり振動する) ことがわかる。
これは、振り子の振れ幅が大きくなっていることから自然なことと言えるだろう
(ブランコを想像すればよい)。
それに対し、線形化により得られた単振動では、振動の周期は振り子の長さ l だけで決まるのだった
(振り子の周期は本講義では解説しておらず、皆さんの物理学の知識に基づいて考える必要がある)。
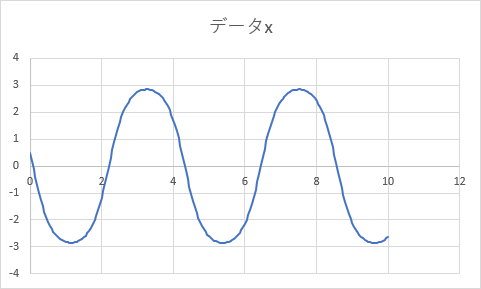
さて、初速度をさらに大きくしてみよう。下図のように初速度を -7 [rad/s] としてみよう。

「データ作成」ボタンをクリックするとグラフは以下のように変化する。
グラフは明らかに振動していない。何が起こっているのだろうか?
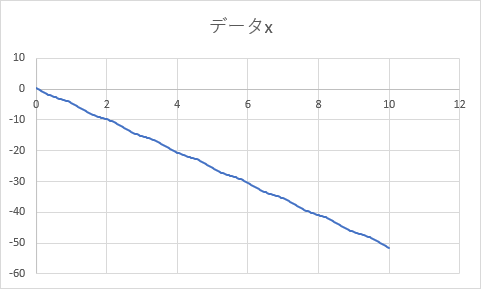
振り子は角度のマイナス方向 (時計周り) に運動をはじめる。
-2π [rad] (およそ -6.28) で振り子が 1 周したことを表す。
-4π [rad] (およそ -12.57) で 2 周、-6π [rad] (およそ -18.85) で 3 周…である。
グラフは -50 [rad] 程度まで角度が変化しているので、振り子がおよそ 8 周したところを表しているのである。
上がって下がって…という脈動のような現象が 8 回起こっていることも読みとれる。
←線形と非線形/非線形制御の例→
Excel VBA で微分方程式をシミュレーションしように戻る

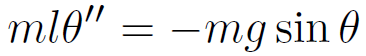
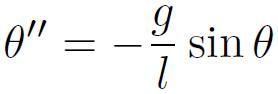

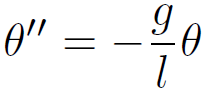


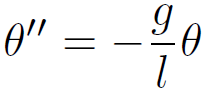





 が成り立つ範囲を大きく逸脱している。
が成り立つ範囲を大きく逸脱している。