

: [問題] 符号付き数の乗算
: 乗算と除算
: 乗算と除算
簡単のために符号なし数の乗算を考えよう。
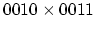 の
計算を行なうには、10 進数のときと同様に筆算で行なうことができる
(図 7)。
の
計算を行なうには、10 進数のときと同様に筆算で行なうことができる
(図 7)。
図 7:
筆算による乗算の実行。
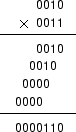 |
一般に 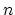 ビットの 2 進数と
ビットの 2 進数と 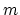 ビットの 2 進数を掛け合わせると、
ビットの 2 進数を掛け合わせると、
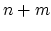 ビットになる
(図 7 では 4 ビット
ビットになる
(図 7 では 4 ビット  4 ビットが 7 ビットに
なっているが、最上位ビットから桁上がりが生ずることも考えられ、
その場合は 8 ビットになるのである)。
4 ビットが 7 ビットに
なっているが、最上位ビットから桁上がりが生ずることも考えられ、
その場合は 8 ビットになるのである)。
図 8:
乗算の第一のアルゴリズムの流れ図。
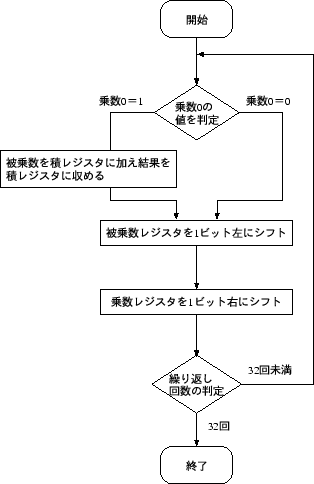 |
以上の筆算をアルゴリズムとしてまとめると図 8
のようになる
(教科書、授業での「第一のバージョン」に相当)。
これはもっとも単純な乗算の実装の例である。
また、このアルゴリズムを
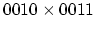 に適用したのが図 9
である。
に適用したのが図 9
である。
図 9:
第一の乗算アルゴリズムを 4 ビットの乗算に適用した様子。
![\begin{figure}\begin{tabular}{c\vert l\vert c\vert c\vert c}
サイクル & ステップ...
...x{3.2ex}[0pt]{4} & (c) & 0000 & 0010 0000 & 0000 0110
\end{tabular}
\end{figure}](img37.png) |
MIPS CPU にこのアルゴリズムを実装するには
- 64 ビット ALU
- 乗数用 32 ビットレジスタ
- 被乗数用 64 ビットレジスタ
- 積用 64 ビットレジスタ
が必要になる。
実際にはアルゴリズムに工夫が加えられ、
- 32 ビット ALU
- 被乗数用 32 ビットレジスタ
- 積用 64 ビットレジスタ (乗数と共用)
のように、乗算ハードウェアはより簡単に実現されている
(教科書、授業における「最終バージョン」)。
そのアルゴリズムの詳細は教科書や授業を参照して欲しいが、
基本は上で見た筆算によるアルゴリズムである。
[問題]
- 図 9 の空欄 (a), (b), (c) は、流れ図 8 において何に対応しているか。
平成16年12月13日
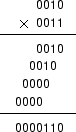
![]() ビットの 2 進数と
ビットの 2 進数と ![]() ビットの 2 進数を掛け合わせると、
ビットの 2 進数を掛け合わせると、
![]() ビットになる
(図 7 では 4 ビット
ビットになる
(図 7 では 4 ビット ![]() 4 ビットが 7 ビットに
なっているが、最上位ビットから桁上がりが生ずることも考えられ、
その場合は 8 ビットになるのである)。
4 ビットが 7 ビットに
なっているが、最上位ビットから桁上がりが生ずることも考えられ、
その場合は 8 ビットになるのである)。
![]() に適用したのが図 9
である。
に適用したのが図 9
である。