 |
[1 ビットの加算 (半加算、全加算)]
論理回路などの授業で学んだように、 加算を行なうには下位ビットから順に 1 ビット ずつ加算を行なってゆけば良い (簡単な復習が 付録 A にある)。
その際、各ビットの加算には「和」と 上位ビットへの「桁上がり (carry out)」の 2 つの出力があることを思い出そう。 さらに、最下位ビット以外のビットの加算には、 下位ビットからの「桁上がり (carry in)」も考慮にいれなければならない のであった。
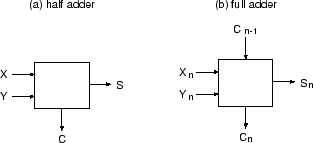
以上を考慮すると、 1 ビットの加算を行なうには、 下位ビットからの桁上がりを考慮しない「半加算器」 と 下位ビットからの桁上がりを考慮する「全加算器」が考えられる (図 2)。
 |
![]() ビットの加算を行なう際、最下位ビットの加算は半加算器で、
それ以外のビットの加算は全加算器で実現できることに注意しよう。
ビットの加算を行なう際、最下位ビットの加算は半加算器で、
それ以外のビットの加算は全加算器で実現できることに注意しよう。
[問題] (論理回路の復習)
全加算器は半加算器 2 つと OR ゲートを用いて構成できる。
余力があれば考えてみてほしい。
[![]() ビットの加算器への拡張]
ビットの加算器への拡張]
前節で触れたように、
![]() ビットの加算器は 1 ビットの加算器 (半加算器や全加算器) を
組み合わせることで構成できる。
ビットの加算器は 1 ビットの加算器 (半加算器や全加算器) を
組み合わせることで構成できる。
[問題]
図 2 の半加算器と全加算器の模式図を用いて、
![]() ビットの加算器を実現してみよ。(ここで構成した
ビットの加算器を実現してみよ。(ここで構成した ![]() ビット加算器は ripple carry adder と呼ばれる)
ビット加算器は ripple carry adder と呼ばれる)