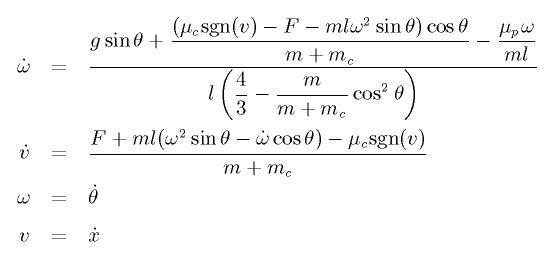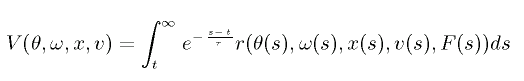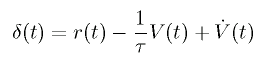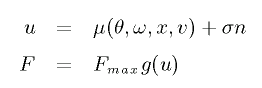Cart-Pole Balancing by Reinforcement Learning



After downloading cp_rl_app.jar, please execute it by double-clicking, or typing "java -jar cp_rl_app.jar".

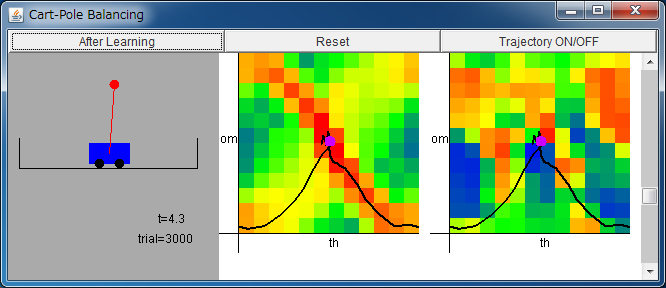
From left: State of the pendulum / Critic / Actor

By pressing "After Learning" button, parameters are set to the values that are obtained after 3000 trials.

The range of horizontal axes of critic/actor is -π <θ < π, and the range of vertical axes of critic/actor is -2.5π <ω < 2.5π where x=v=0.
The colors of the approximated functions denote the following values.
blue: negative, green: 0, red: positive.

By clicking the fields of critic/actor, you can set the initial state of the pendulum.
By regulating the scroll bar, you can change the value of mass.

If the above application does not start, please install OpenJDK from adoptium.net.

Let us consider a cart-pole balancing task using the reinforcement learning.
The dynamics of the cart-pole system with a force F is written as



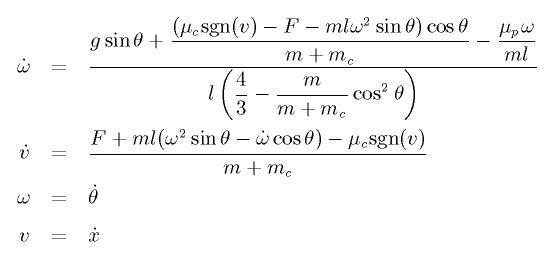
Our goal is to construct a controller which observes the state (θ, ω, x, v) of the system and gives an appropriate value of force F to the cart to obtain the upright state of the pole.

Under the scheme of the reinforcement learning, the controller can be constructed as shown in the following figure.




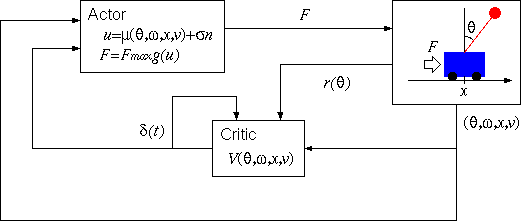
The reward r is defined as r(θ) = cos θ so that the upright state receives a maximal reward.
The cumulated future reward following the policy F is defined as



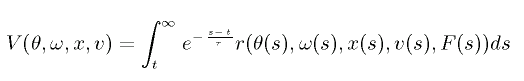
By searching large values of V(θ, ω, x, v), we can obtain the upright state of the pendulum.

However, V(θ, ω, x, v) is an unknown function, so we must perform a function approximation to obtain V(θ, ω, x, v).
It is known that V(θ, ω, x, v) can be correctly learned by minimizing the temporal difference error δ(t).



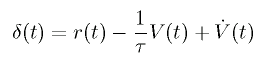
The unit which approximates V(θ, ω, x, v) is called "critic".
On the other hand, the unit which determines the input F according to (θ, ω, x, v) is called "actor" (n is a noise).



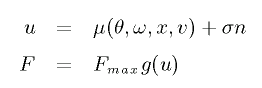
μ(θ, ω, x, v) is also an unknown function, we must perform a function approximation for μ(θ, ω, x ,v).
Also in this case, μ(θ, ω, x, v) can be correctly approximated by minimizing the temporal difference error δ(t).

In this applet, for the learning of the critic, we use TD(λ) method for continuous time and space, and, for the learning of the actor, we use policy gradient method.

This page is based on the following papers.


<< Manual Control of Bipedal Walking / Swinging up a Pendulum by Reinforcement Learning >>

Back to Takashi Kanamaru's Web Page