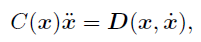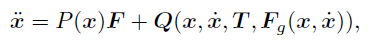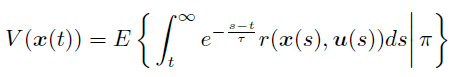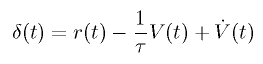強化学習による CPG 入力下二足歩行モデルの制御
bc_rl_app.jarをダウンロードしてダブルクリックして実行してください(コマンドラインでは java -jar bc_rl_app.jar)。
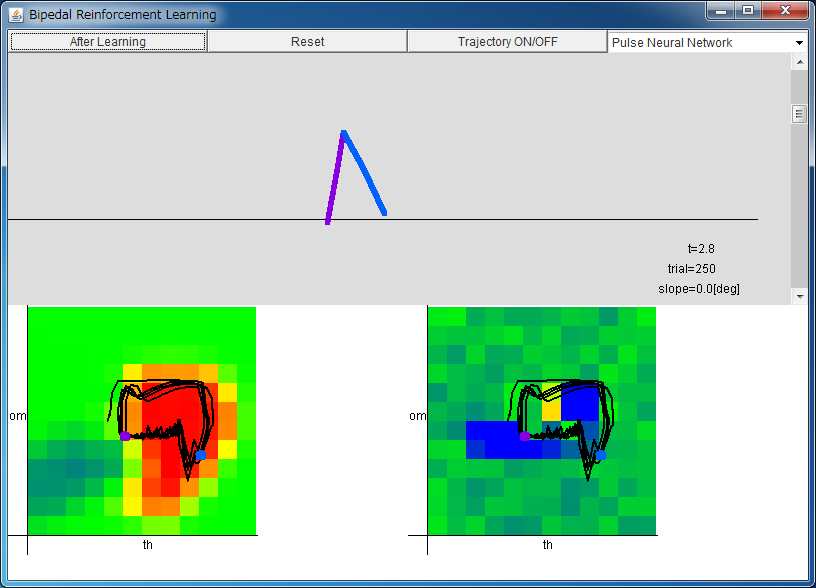
左から順に Critic、Actor。
「After Learning」ボタンを押すと、学習が完了した状態にセットされます。
Critic/Actor は 横軸は -1 <θ < 1、
縦軸は -8.0 <ω < 8.0 を表す。
値は、青：負、緑：0、赤：正を表す。
シミュレータが実行出来ない方は adoptium.net からOpenJDKをインストールしてください。
Taga (1991) らが用いた二次元平面上の二足歩行モデルの歩行を強化学習により
獲得することを考えます。
なお、こちらのページでは同じモデルの手動制御を体験できますので合わせて御覧ください。
Taga (1991) らの二足歩行モデルは、8個の制約条件
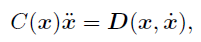の元での14変数についての運動方程式
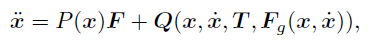で書き表せます。
14 - 8 = 6 ですから、このモデルの位置は
腰の位置 (x, y) および
両足の腰と膝の角度
(θR1, θR2,
θL1, θL2)
の計6変数で表せます。
さらにこれらの時間微分
(vx, vy) および
(ωR1, ωR2,
ωL1, ωL2)
も考慮することで力学系としての系の状態が指定されます。
ここで、この二足歩行モデルに与えるトルク T は
PD 制御則により決定されるとし、
各関節の目標角 θd は生体を模倣して
Central Pattern Generator (CPG)
：中枢パターン発生器の出力であるとします。
ここで、CPG としては Kanamaru (2006) のパルスニューラルネットワークの
集団発火率、および結合 van der Pol 方程式の出力のどちらかを選択できます。
松原 (2005) らに基づき、下図のような構成で強化学習による制御則の獲得を目指します。
制御則の出力としてはパルスニューラルネットワークの結合強度を選びます。
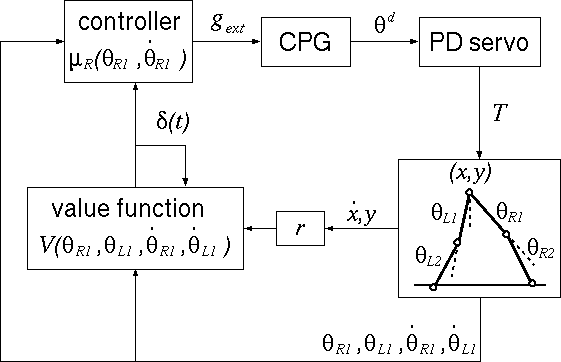
まず、系の状態に応じた報酬 r は
「腰の高さが一定」および「水平方向の速度が一定」の時に
最大となるように定めます。
このとき、制御則 π に従った時に期待される報酬
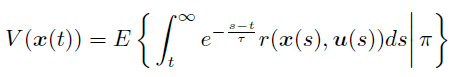は変数 (θR1, θL1,
ωR1, ωL1) の関数で書き表せるとします。
V(θR1, θL1,
ωR1, ωL1)
が大きくなるように制御を行うと、系は二足歩行を獲得することになります。
しかし V(θR1, θL1,
ωR1, ωL1) は未知の関数なので、実際には関数近似を行って推定することになります。
このとき、以下の TD 誤差が小さくなるようにパラメータの変更を行うと、
V(θR1, θL1,
ωR1, ωL1) が推定されます。
このように、V(θR1, θL1,
ωR1, ωL1) を推定するユニットを Critic と呼びます。
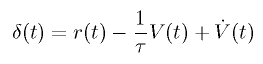一方、モデルの状態に応じて制御入力を決めるユニットを
Actor と言いやはり関数近似により推定します。
ここでは、Critic の学習に連続時間、連続空間の TD(λ) 法、
Actor の学習に方策こう配法を用いています。
現実のロボットへの応用を目指しているため計算の高速化が重要であり、
そのために様々な工夫をしています(未発表)。
このページは以下の文献を参考にしています。
- [用いた CPG について]
Takashi Kanamaru,
"Analysis of synchronization between two modules of pulse neural networks with excitatory and inhibitory connections,"
Neural Computation, vol.18, no.5, pp.1111-1131 (2006). (preprint PDF)
Takashi Kanamaru,
"van der Pol oscillator", Scholarpedia, 2(1):2202.
- [強化学習による CPG入力下二足歩行モデルの制御について]
松原崇充、森本淳、中西淳、佐藤雅昭、銅谷賢治
"方策こう配法を用いた動的行動則の獲得：2 足歩行運動への適用"
電子情報通信学会論文誌, D-II, vol.J88-D-II, 53-65 (2005).
T. Matsubara, J. Morimoto, J. Nakanishi, M. Sato, and K. Doya
"Learning CPG-based Biped Locomotion with a Policy Gradient Method"
Robotics and Autonomus Systems, vol. 54, issue 11, pp. 911-920 (2006).
- [二足歩行モデルについて]
G. Taga, Y. Yamaguchi, and H. Shimizu,
"Self-organized control of bipedal locomotion by neural oscillators in unpredictable environment"
Biological Cybernetics, vol. 65, pp.147-159 (1991).
- [強化学習について]
Kenji Doya
"Reinforcement Learning in Continuous Time and Space"
Neural Computation, vol.12, 219-245 (2000).
「二足歩行モデルの手動制御」へ→
金丸隆志のページに戻る