電気結合を持つパルスニューラルネットワークにおける
Stochastic Synchrony of Chaos
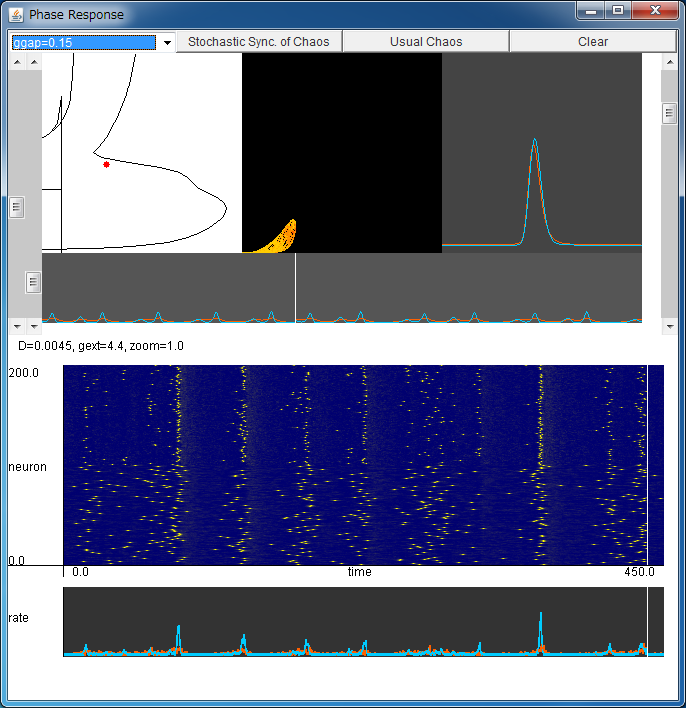
ssync.jarをダウンロードしてダブルクリックして実行してください(コマンドラインでは java -jar ssync.jar)。
シミュレータが実行出来ない方は adoptium.net からOpenJDKをインストールしてください。

 |
パラメータ設定 |
フィールド上をクリックすることで、 ノイズ強度 D (横軸) と集団間結合強度 gext=gEI=gIE (縦軸) を設定できます。 パラメータの値によって、同期振動やカオス的同期振動が見られます。 パラメータは左の2つのスクロールバーでも変更できます。 |
 |
(JE,JI) |
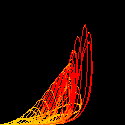
(JE,JI) 平面における集団的発火頻度 JE,JI の変化を観察できます。 カオスアトラクターも見られます。 また、右側のスクロールバーでズームイン/アウトできます。 |
 |
(nE,nI) |
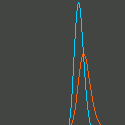
興奮性および抑制性集団の確率分布の時間変化を表示します。 赤が興奮性集団、青が抑制性集団を表します。 |
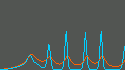 |
JE(t)、 JI(t) の時間変化 |
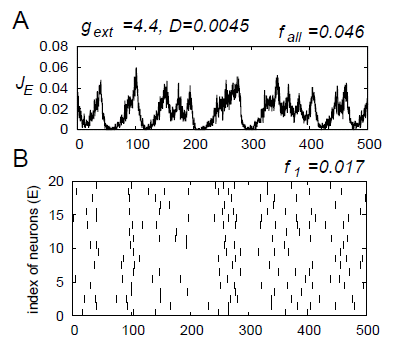
興奮性および抑制性集団の集団的発火頻度 JE(t)、 JI(t) の時間変化を表示します。 赤が興奮性集団、青が抑制性集団を表します。 下の NE=NI=100 なる系のシミュレーションと対応します。 |
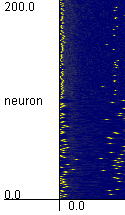 |
NE=NI=100 なる系のシミュレーション |
NE=NI=100 なる系の発火時刻を黄色でプロットします。 1 から 100 が興奮性ニューロン、101 から 200 が抑制性ニューロンです。 |
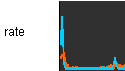 |
NE=NI=100 なる系の集団的発火頻度 |
NE=NI=100 なる系の集団的発火頻度の時間変化を表示します。 上の JE(t)、 JI(t) に対応します。 赤が興奮性ニューロン、青が抑制性ニューロンです。 |
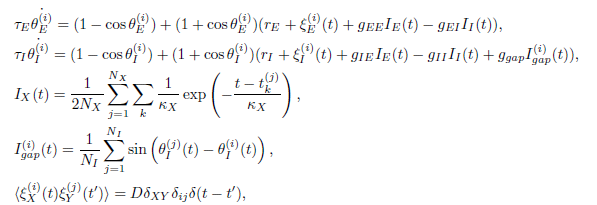
 相互作用 IX(t) は、素子がパルスを出力したときに他の素子に影響が及ぶようになっており、これは化学シナプスと呼ばれる結合をモデル化しています。
相互作用 IX(t) は、素子がパルスを出力したときに他の素子に影響が及ぶようになっており、これは化学シナプスと呼ばれる結合をモデル化しています。
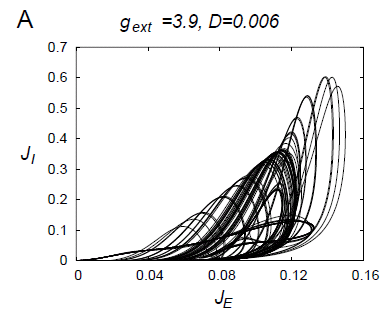
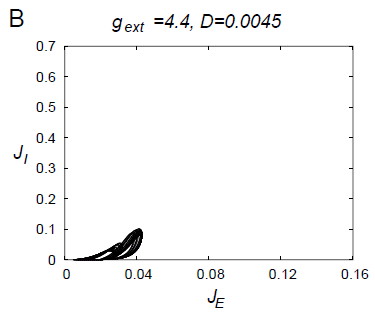 フォッカー・プランク方程式の解析によると、この系には上図に表されるような
低次元カオスが存在することがわかります。
フォッカー・プランク方程式の解析によると、この系には上図に表されるような
低次元カオスが存在することがわかります。