Analysis of Synchronization in Pulse Neural Networks with Phase Response Function



After downloading pr.jar, please execute it by double-clicking, or typing "java -jar pr.jar".

If the above application does not start, please install OpenJDK from adoptium.net.



Explanation of Applet

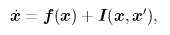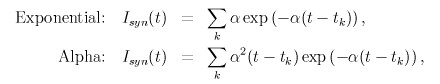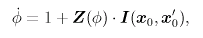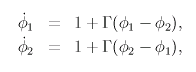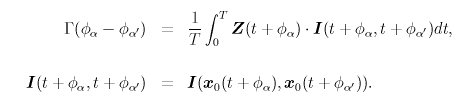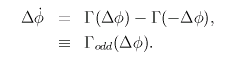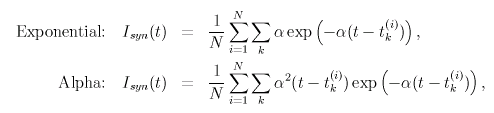
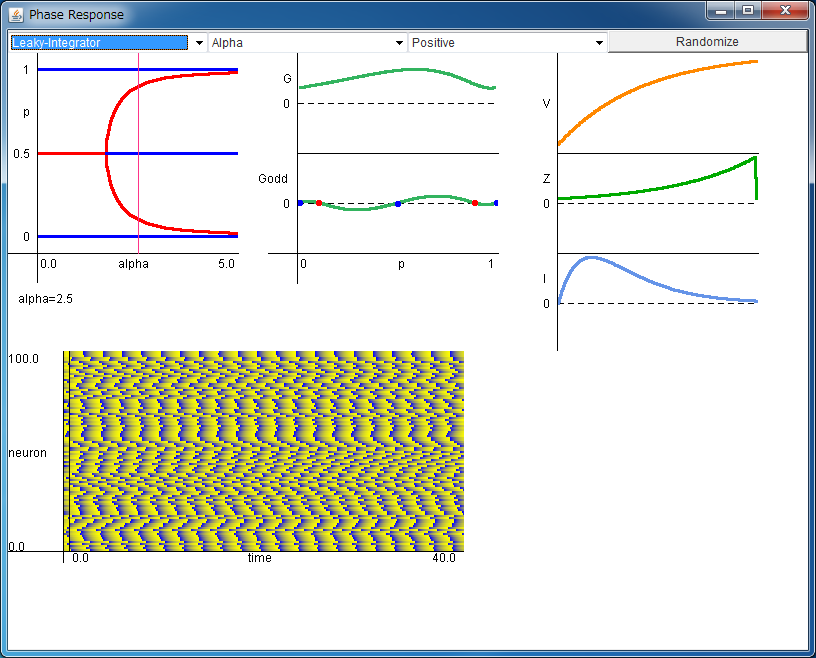
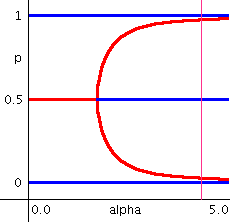
 (α,Δφ) The dependence of the stationary phase difference Δφ (denoted as "p") on the synaptic rate α is shown.
The red lines show the stable phase differences, and the blue lines show the unstable phase differences.
The form of lines changes according to the neuron models.
By clicking the field, you can change the value of synaptic rate α (The pink line show the present value of α.).
By clicking the outside of the field, the pink line disappears.
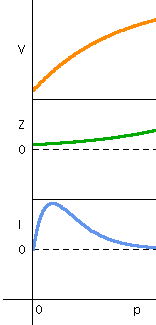
V(φ), Z(φ), I(φ) The membrane potential V(φ) of the neuron, the phase response Z(φ), and the synaptic input I(φ) are shown.
The waveform of I(φ) changes according to the value of the synaptic rate α.
You can regard the phase φ as the time t.
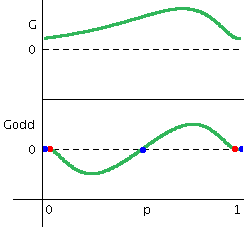
Γ(φ), Γodd(φ) Γ(φ) and Γodd(φ) calculated from Z(φ) and I(φ) are shown.
The intersections of Γodd(φ) and the horizontal axis show the stationary phase differences Δφ,
and the red circles and the blue circles show the stable and unstable phase differences, respectively.
This graph corresponds to the graph in (α,Δφ) plane.
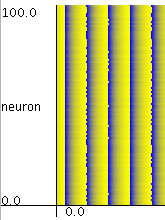
Simulation of the network with 100 neurons. When the synchronized solution (Δφ=0) is stable, all neurons tend to synchronize with each other.


We treat two oscillatin neurons interacting with weak couplings. For simplicity, let us define the dynamics of one neuron as



where f(x) governs the dynamic of neuron x, and I(x,x') is the synaptic input from the other neuron.

The synaptic inputs are often modeled by a sum of exponential functions or alpha functions.



where tk is the k-th firing time of this neuron and α is the synaptic rate.

Generally, weakly coupled two oscillators can be reduced to the phase model written as



where Z(φ) is the phase response function that shows the change in frequency caused by a small perturbation.

After averaging, the dynamics of weakly coupled two neurons follow the phase model written as



where Γ(φ) can be calculated by the following formula.



The dynamics of the phase difference Δφ of two oscillating neurons can be analyzed by investigating the following model. Note that the stationary phase difference Δφ satisfies Γodd(Δφ)=0, and its stability can be determined by the sign of the slope.



You can perform analyses of synchronization in pulse neural networks using the phase response function. You can choose various neuron models and synaptic inputs. Pulse neural networks are composed of 100 neurons, and their connections are global as follows.



When the stationary phase difference with Δφ=0 is stable, neurons tend to fire synchronously.

The definitions of neuron models are shown in this page.

This page is based on the following papers.
<< FitzHugh-Nagumo Equation / Chaos in a Pulse Neural Network : Analysis of Synchronization with the Fokker-Planck Equation >>

Introduction to Chaos and Nonlinear Dynamics