Parametric Pendulum

After downloading ppendulum.jar, please execute it by double-clicking, or typing "java -jar ppendulum.jar".

If the above application does not start, please install OpenJDK from adoptium.net.

Snapshot 1 / Snapshot 2 / Snapshot 3 of the small version

Explanation of This Simulator

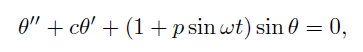
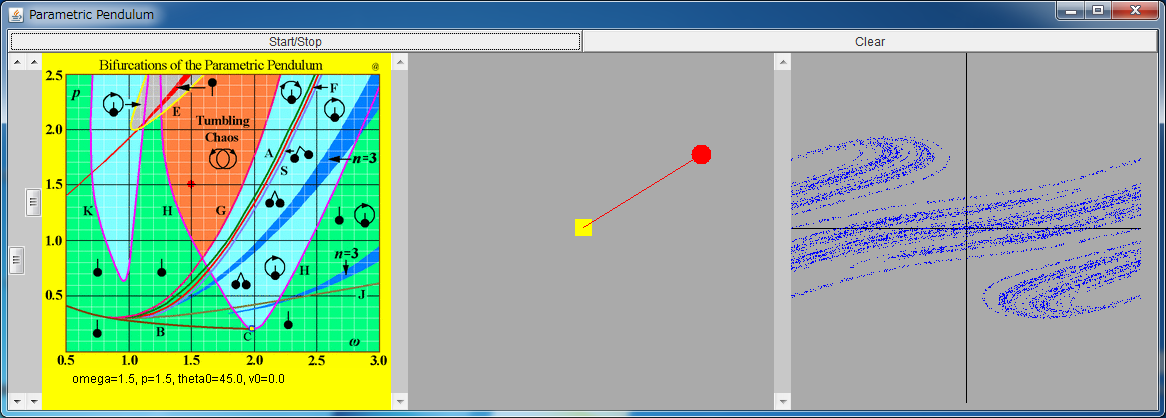
	Bifurcation sets	By clicking this field, you can change the values of the parameters (ω, p). Also by regulating the two left bars, you can regulate them.
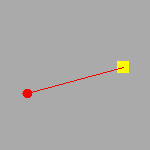
	Movement the parametric pendulum	The dynamics of the parametric pendulum is shown. After stopping the motion of the pendulum by pressing the "Start/Stop" button, you can change the angle θ and the angular velocity θ' of the pendulum with two bars.
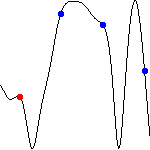
	The relative height of the pendulum (only for the huge version)	The temporal change of the relative height of the pendulum (-cos θ) is shown. At t=2nπ/ω (n : integer), red and blue points are drawn when θ>0 and θ<0, respectively.
	Poincare section	(θ , θ') at t=2nπ/ω (n : integer) is plotted.

The dynamics of a parametric pendulum is defined as

with c=0.1. This equation models the dynamics of a pendulum whose fulcrum is periodically moved in the vertical direction.
You can see the dynamics of the fabricated parametric pendulum in the "Driven Pendulum" movie.

The dynamics of this parametric pendulum show chaos when the values of the parameters and the initial conditions are appropriately chosen. Moreover, the upsidedown state of the pendulum becomes stable when the values of the parameters and the initial conditions are appropriately chosen.

<< Attractor of Duffing Equation / Various Pendulums >>

Introduction to Chaos and Nonlinear Dynamics