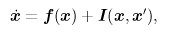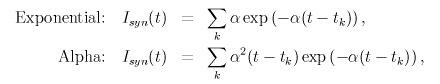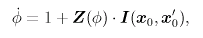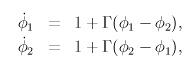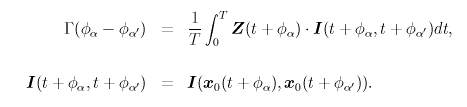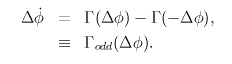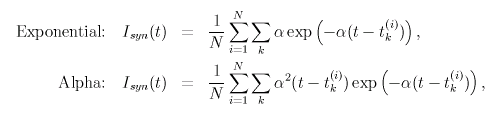位相応答関数を用いたパルスニューラルネットワークの同期解析
pr.jarをダウンロードしてダブルクリックして実行してください(コマンドラインでは java -jar pr.jar)。
シミュレータが実行出来ない方は adoptium.net からOpenJDKをインストールしてください。

|
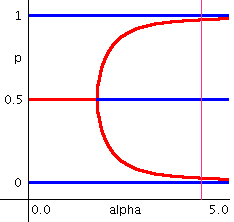
(α,Δφ) |
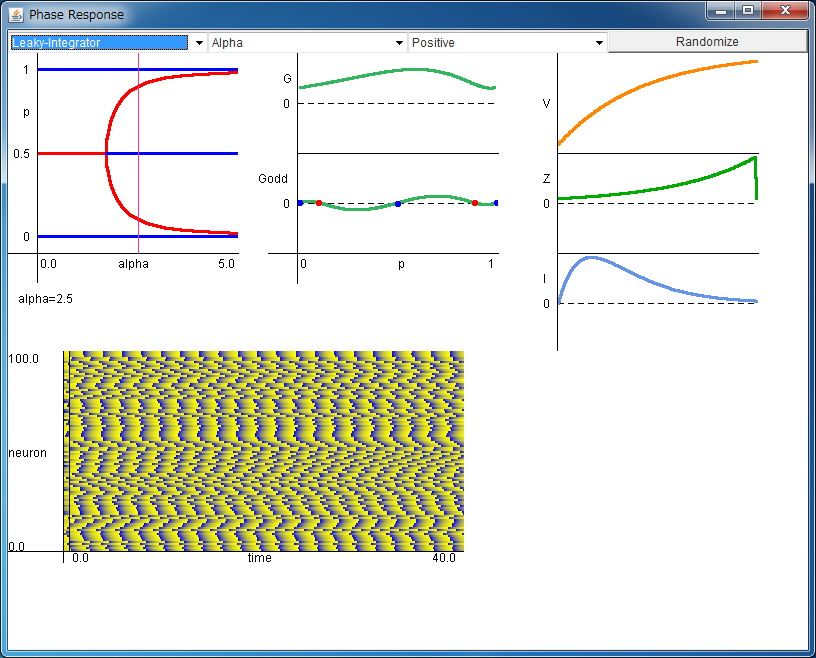
定常な位相差 Δφ (p で表示)のシナプス定数 α への依存性をプロットします。 赤が安定な位相差、青が不安定な位相差です。 選んだモデルやシナプス波形によって変化します。 フィールド上をクリックすると、シナプス定数 α を決定できます (ピンクの線は現在の α)。 フィールド外をクリックすると、ピンクの線は消えます。 |

|
V(φ), Z(φ), I(φ) |
ニューロンの膜電位 V(φ)、位相応答 Z(φ)、シナプス入力 I(φ) 表示します。 シナプス定数 α の値に応じて、シナプス入力の波形は変化します。 位相 φ と時刻 t は同一視できます。 |
|
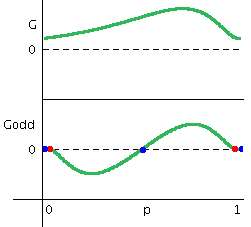
Γ(φ), Γodd(φ) |
Z(φ) と I(φ) から計算される
Γ(φ) と Γodd(φ) を表示しています。 Γodd(φ) と横軸の交点が定常な位相差を表しており、 赤丸が安定な位相差、青丸が不安定な位相差です。(α,Δφ) 平面と対応しています。 |
|
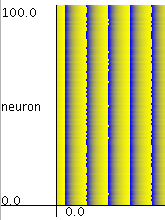
ニューロン 100 個を結合させた系のシミュレーション | 同期解 (Δφ=0) が安定であれば、全素子は同期する傾向にあります。 |