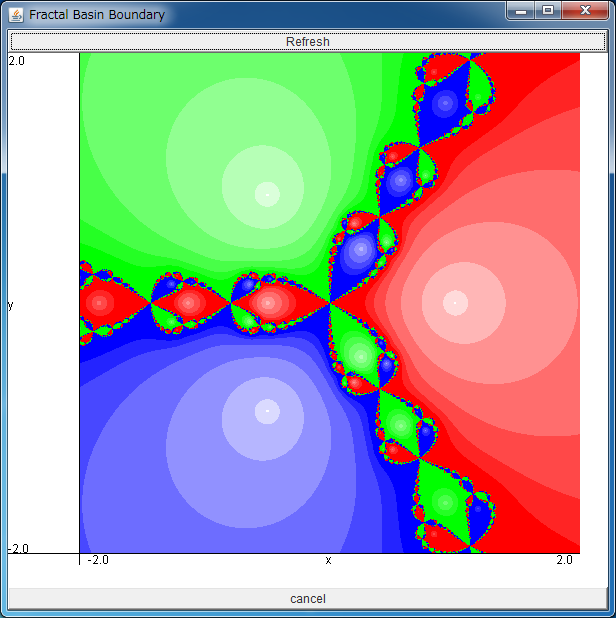
まず、正しい解 (x,y) = (1, 0)、(-1/2, √3/2)、(-1/2, -√3/2)
がそれぞれ 3 つの白い円の中心に表示されています。
そして、それぞれに収束する初期点が赤、緑、青に色分けされています。
色が白いほど、速く正しい解に収束することを意味します。
ひとめ見てわかるように、各解に収束する初期点の境界は非常に複雑な
構造をしています。
マウスを用いて拡大するとわかりますが、境界はフラクタル的な性質を持っており、
どこまで拡大しても、境界は常に複雑さを保ったままです。
アトラクターに引き込まれる初期点の集合をベイスンと呼びますが、
ここでみたようにフラクタル的な性質を持ったベイスンの境界のことを
フラクタル・ベイスン境界と呼びます。
ここで扱ったモデルは抽象的な数学モデルですが、
フラクタル・ベイスン境界は現実の物理系でも起こることが知られています。
これは、系に複数の安定状態があり、初期点がフラクタルなベイスンの境界付近にあるとき、
初期点を無限の精度で調べないと、系の最終的な状態は予言しえないことを
意味します。
この事実は物理学に大きなインパクトを与えたことに注意しましょう。
さらに、アトラクターがカオスであるときは、いたるところでベイスンが
混じりあっているという病的な状態も起こり得ることが知られています。
そのようなベイスンはリドル・ベイスンとよばれ、
これもシミュレータで調べることができます。
なお、このページのシミュレータのフラクタルな境界上には、
いつまでも正しい解に収束しない「周期軌道」や「カオス軌道」
も存在することが知られています。
しかし、それらはアトラクターではなく、ルベーグ測度も 0 なので、
いくら拡大しても観測することは難しいでしょう。
|