マンデルブロー集合 for Android
|
保存した画像を壁紙に
|
色の変更
|
|

|
ダウンロード (android 4.1 以降対応)
Google Play よりダウンロード
[操作方法]
- 画面を2本指でタッチして動かすことで、拡大・縮小を行うことができます。
- Menu ボタンを押すと、以下の操作を行えます。
- 領域リセット : 集合をデフォルトの状態に戻します。
- 色の変更 : 4 通りのカラーモードを選択できます。
- 拡大率 : 拡大率を変更できます。
- 画像の保存 : 画像を保存します。
[解説]
複素平面上の写像
z n+1 = zn2 + c
を考えましょう。
このとき初期点 z0=0 から出発した軌道は、複素パラメータ c に依存して固定点、
周期解、カオス解などに収束する場合と、
無限大に発散する場合が考えられます。
無限の時間が経過しても軌道が発散しないパラメータ c の集合は
マンデルブロー集合と呼ばれます。
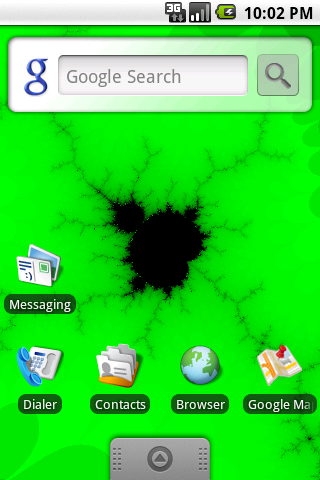
このシミュレータは複素平面上でマンデルブロー集合を図示します。
シミュレータ上で黒い領域がマンデルブロー集合です。解が発散する領域は、
発散までにかかる時間によって決まる色がつけられています。
マウスによって図を拡大すると、マンデルブロー集合は無限に
細かい構造を持っていることがわかります。
この図形に見られるように、「部分に全体が無限に含まれている」ような
自己相似構造を持った図形をマンデルブローは「フラクタル」と名付けました。
後の研究により、マンデルブロー集合の境界の次元は 2 であることや
境界は連結していることなどが宍倉光広教授により数学的に証明されました。
一般に、フラクタル図形は非整数次元を持つことが多いですから、
マンデルブロー集合はフラクタルの典型例ではないことになります。
しかし、マンデルブロー集合がフラクタルやカオスの研究に与えたインパクトは大きく、
記念碑的な図形として今でもしばしば紹介されます。
このページは以下の書籍を参考にしています。
合原一幸、黒崎政男「哲学者クロサキと工学者アイハラの神はカオスに宿りたもう」
「フラクタルベイスン境界 for Android」へ→
カオス&非線形力学入門に戻る

